Loading [MathJax]/extensions/tex2jax.js

精密計測

スティッチング測定

スティッチング測定 ( Stitching Measurement )とは部分測定を合成して全体形状を得る測定方法である。測定領域を拡大するだけでなく、被測定物の形状自由度を拡大し、測定精度の向上も可能なことが示されている。

詳細

経緯

　光学素子の形状測定において、部分測定を合成して全体形状を得るスティッチング測定は、測定領域の拡大を目的として干渉計をベースに研究が開始された[1]。この技術のポイントは、部分測定データに含まれる位置姿勢誤差を推定し除去することである。実用的な精度でこの課題を解決したのは、オーバーラップ部分のミスマッチが最小になるように位置姿勢誤差を計算する方法だった[2,3]。この方法が確立すると実用化が進展し、望遠鏡用大口径ミラーの製作[4]、Ｘ線用の高精度光学面の評価[5]へと応用が広がった。
　また、スティッチング測定を使えば１回の測定領域を分割して狭くできることを利用し、干渉計を使った非球面計測が可能になった。自動的に小径の測定領域をスティッチ測定する干渉計が市販されている[6]。さらに被測定物を回転させたまま、高速に測定する装置も提案されている[7]。
　スティッチングを干渉計以外の測定法と組み合わせた研究も進んでおり、干渉計よりも大きな波面変化を測定できるシャックハルトマンセンサを用いる方法[8]、参照波面を微調整しながら部分測定する方法などが実用化されている[9]。さらにプローブを用いた３次元座標測定装置など、点計測装置への応用も提案されている[10]。
　３次元立体計測に対しては、円筒近似できるという制約条件つきながら、全周360度の分割測定が実現できている[11,12]。
　スティッチング測定の重要なもう一つの側面は、測定装置が固有に持っている系統誤差、すなわち各測定データに共通に現れる誤差もスティッチパラメ－タに加えることによって推定し除去できることである。その結果、全面を一括測定する場合よりも不確かさを低減できる[6]。
　このように、スティッチ技術は測定領域を拡大するだけでなく、被測定物の形状自由度を拡大し、測定精度の向上も可能な技術として発展を続けている。一方で市販装置にも搭載される普及した技術ともなっている[6,13]。

アルゴリズム

　スティッチング測定には次の４つのポイントがある。

(1) 部分測定領域の配置方法

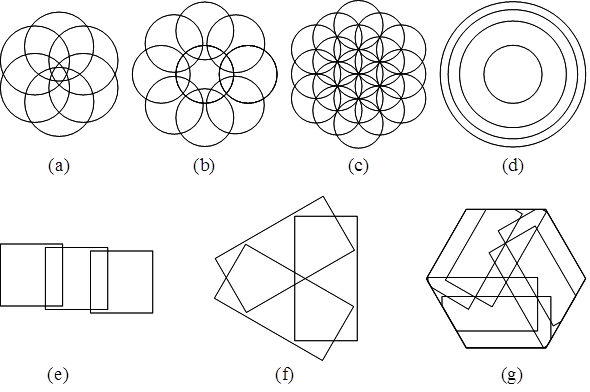
　図１に部分測定領域の配置例を示す。(a)と(b)は円形の部分測定領域を同心円状に走査した例、(c)は綴れ折状に走査した例である。軸対称非球面を干渉計で測定すると曲率が合致する輪帯状の干渉縞が得られる。(d)はこの輪帯状の干渉縞を合成する例である。また矩形領域のスティッチング測定についてはＸＹ走査した例(e)、被測定物を回転した例(f)、それらを組み合わせた例(g)がある。

(2) 評価関数の構成方法

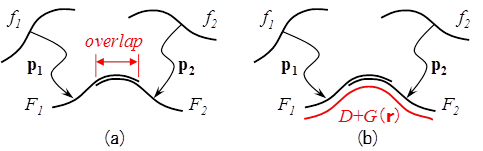
　測定対象や装置によって様々な提案があるが、多用されるのはオーバーラップ部のミスマッチを評価関数とする方法である。図２(a)に示すように２つの測定結果 \( f_1 \) と \( f_2 \) から位置姿勢誤差の P\( _1 \) と P\( _2 \) を除去し、形状 \( F_1 \) と \( F_2 \) を得る。この時、オーバーラップ部における \( F_1 \) と \( F_2 \) を補間してミスマッチを計算し、これが最小になるように P\( _1 \) と P\( _2 \) を推定計算する。
　一方、この方法は測定データの一部だけを使って推定計算するので、測定点数の少ない点計測方式の装置では補間誤差が大きな問題となる。これに対し、図２(b)に示す提案がある[10]。設計形状 \( D \) とパラメータ \( r \) を含む関数 \( G(r) \) を形状 \( F_1 \) 、\( F_2 \) にフィットさせて P\( _1 \) と P\( _2 \) および \( r \) を推定する。設計形状の非球面量が大きいほど推定誤差が小さくなるという特徴がある。

図1 部分測定領域の配置例
図2 評価関数の構成方法

(3) 評価関数の最適化方法

　多用されるのは最小２乗法を用いて評価関数を最適化し、パラメータを求める方法である。その他ではシンプレックス法を採用した例もある。パラメータの存在範囲が既知の場合には制約条件付きの最適値問題となる。

(4) 部分測定結果を合成する方法

　位置姿勢誤差を補正した部分形状 \( F_1 \) と \( F_2 \) を補間し、平均化して合成し、全面のデータとする。

関連項目

引用

  1. C. J. Kim: Polynomial fit of interferograms, PhD Dissertation, University of Arizona (1982).
  2. W. M. Cheng and M. Chen: Transformation and connection of subapertures in the multiaperture overlap-scanning technique for large optics tests, Opt. Eng. , 32, 8 (1993) 1947.
  3. M. Otsubo, K. Okada and J. Tsujiuchi: Measurement of large plane surface shapes by connecting small-aperture interferograms, Opt. Eng. , 33, 2 (1994) 608.
  4. C. Zhao and J.H. Burge: Stitching of off-axis sub-aperture null measurements of an aspheric surface, Proc. SPIE, 7063 (2008) 706316-1.
  5. 湯本博勝，三村秀和，木村隆志，大橋治彦，他：SPring-8における大型X線ミラーのためのスティッチング干渉計測法に基づく高精度表面形状計測装置の開発，精密工学会秋季大会講演論文集 (2009) 141.
  6. J. Fleig, et. al. : An automated subaperture stitching interferometer workstation for spherical and aspherical surfaces, Proc. SPIE, 5185 (2003) 296.
  7. C.W. Liang, H.S. Chang, P.C. Lin, C.C. Lee and Y.C. Chen: Vibration modulated subaperture stitching interferometry, Opt. Exp., 21, 15(2013), 18255.
  8. 吉武康裕，吉田実，針山達雄：シャックハルトマンセンサの画像による波面収差繋ぎ測定技術，精密工学会誌, 77, 7 (2011) 676.
  9. 近藤余範：表面形状の計測技術と標準に関する調査研究，産総研計量標準報告, 8, 3 (2011) 299.
  10. 根岸真人，保坂光太郎，堆浩太郎: 近似参照形状を用いたスティッチ・アルゴリズムの開発, 精密工学会誌, 81, 6(2015) 555.
  11. H. Guo and M. Chen: Multiview connection technique for 360 deg three dimensional measurement, Opt. Eng. , 42, 4 (2003) 900.
  12. 佐藤祐介，笹島和幸，原精一郎: 円筒機能面全体計測に対する新しい接続手法の開発，精密工学会春季大会講演論文集 (2003) 473.
  13. 三浦勝弘、岡田睦、松葉正、古田島秀夫: スティッチングを用いた高ＮＡ非球面レンズの非接触形状計測法, 精密工学会秋季大会講演論文集 (2004) 187.
執　筆 ： 根岸　真人

PV数 : 11

4．精密計測用語