エバネッセント光 ( evanescent light ) は、全反射条件 ( total internal reflection condition ) 下において、低屈折率媒質側にしみ出る特殊な光である。一般的な光のように自由空間を伝搬することはなく、全反射界面から波長程度の領域に局在する特性を有する。

詳細

生成

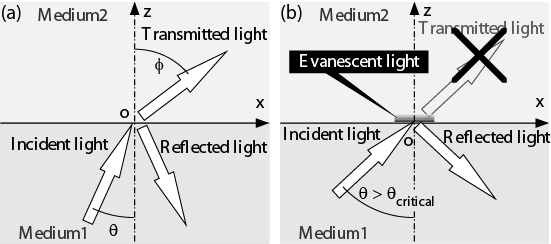
図1にエバネッセント光生成の様子を示す。今、図のように屈折率 ( refractive index ) が離散的に異なる媒質界面に向けて伝搬する光波を考える。一般に、光は自由空間伝搬するが、屈折率が離散的に異なった媒質間の界面においては、反射、透過（屈折）により、反射光 ( reflected light )、透過光 ( transmitted light ) の二波に分離した後、それぞれ両媒質内を伝搬する（図1(a)）。しかし、高屈折率媒質（媒質1）から、低屈折率媒質（媒質2）へ向けて光が伝搬する場合は、必ずしも常に反射光、透過光の二波に分離するのではなく、入射角度によっては透過光が存在しない状況がありうる。具体的には、入射角度 \( \theta \) を大きくしていくと、スネルの法則より屈折角度 \( \phi \) も大きくなっていき、入射角度 \( \theta \) が臨界角度(critical angle) \( \theta_{critical} \) を超えた時に、屈折角度 \( \phi \gt \frac {\pi} {2} \)に達する。これは、媒質2内において自由空間伝搬する光波は存在しないこと、すなわち、すべての入射光波は界面で反射される（全反射）ことを意味する。このように全反射条件下においては、入射光波が有していたエネルギーはすべて媒質1側を自由空間伝搬することになるが、その光エネルギーの存在領域に視点を向けると、光エネルギーは、離散的屈折率界面を厳密な境として媒質1側に閉じこめられているわけではなく（すなわち、光学的反射界面を光エネルギーの存在領域で定義すると、それは、離散的な屈折率界面と一致しない）、媒質2側にも、波長程度の領域分だけ、あたかも媒質1側からしみだしているような形態で存在していることが知られている。この媒質2側にもれだしている光をエバネッセント光という。

記述および特性

エバネッセント光の電場振幅Eは、Maxwellの方程式を起点にして界面における電磁場の境界条件を考慮することにより導出が可能であり、

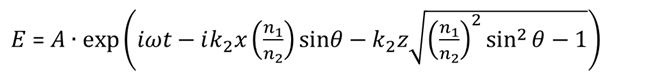
といった形式で記述される。ただし、\( A,ω,k_2,n_1,n_2,\theta \)はそれぞれ、基準振幅、角振動数、媒質2内の波数、媒質1、2の屈折率、入射角度を示し、図1のように \( x-z \)座標をとるものとする。本式において、指数部の第一項は時間的振動を、第二項はこの光波が \( x \)方向のみに伝搬する（伝搬方向に \( z \)成分を有さない）ことを意味する。つまり、エバネッセント光の電場は、一般の光波と同様に時空間において振動するが、その振動は（自由空間伝搬としてではなく）全反射界面沿いに限定した伝搬形態を有している。そして、エバネッセント光の空間的強度分布を与えるのが第三項である。この第三項は、エバネッセント光振幅が、\( z \)方向に対して指数的に急峻に減衰することを示す。以上、第一項から第三項をまとめると、エバネッセント光は、入射光波と同じ振動数で、全反射界面に沿って伝搬する光波であり、そのエネルギー分布は、全反射界面から波長程度の領域に限定され、全反射界面にまとわりつくように局在することが分かる。

可視化

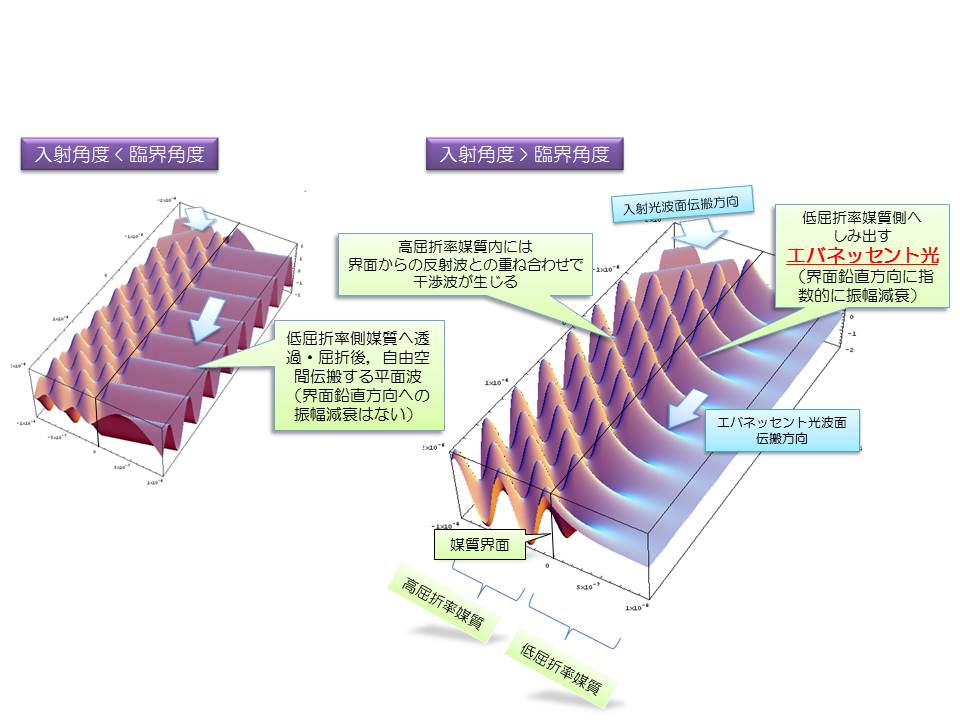
前述のようにエバネッセント光は、全反射界面に局在し、自由空間を伝搬してこないため、直接観察することは原理上、困難（例えば、近接場光学顕微鏡等により微細なプローブをエバネッセント光内に挿入し、その散乱光を取得することで間接的に観察する）となる。そのため、具体的な光波の振る舞いを可視化するためには、計算機シミュレーションが用いられることが多い。図2に計算機シミュレーションにより算出したエバネッセント光電場振幅分布の一例（ここでは入射光波がS偏光時の電場振幅値をプロットし三次元的に俯瞰したもの）を示す。左には、比較のため、入射角度が臨界角度以下のときの同一時空間における電場振幅分布を示している。入射角度が臨界角度より小さいときは、低屈折率媒質内において振幅分布も一様な平面光波が、スネルの法則で決定される屈折角の方向に伝搬していく（自由空間伝搬）のに対して、入射角度が臨界角度より大きくなると、低屈折率媒質内における光波振幅は、指数的に急峻に減衰する。また、その伝搬方向は、界面方向に一致する。なお、高屈折率媒質内においては、入射光波と反射光波が共存するため、それらの重ね合わせによる干渉光波が生成される。特に、エバネッセント光生成時には、全反射により、入射・反射、両光波の光量が一致するため、界面鉛直方向に可視度1の定在波が生成される。このようにエバネッセント光は、ある瞬間で観察すると、波動としての振幅分布が明らかになるが、それらは界面方向に伝搬するため、時間平均をとって観察すると、界面方向には一様な強度分布を示す。

応用

エバネッセント光特有の非自由空間伝搬特性、局在特性を利用することで、通常の光（自由空間伝搬光）とは異なった目的、形態での光エネルギーの活用が可能となる。古くから、基礎科学計測機器への応用が進められてきた。代表的なものとしては、高いSN比での暗視野照明観察が可能であることに着目した近接場光学顕微鏡^[1]や全反射顕微鏡^[2]、また、さらに界面近傍の情報のみを選択的に観察できることを積極的に利用した全反射蛍光顕微鏡^[3]等への適用が挙げられる。

近年は、このような基礎科学計測機器への適用に加えて、精密工学への応用も活発に進められてきている。先端精密加工を実現するための高感度精密計測技術として、半導体微細回路上の異物検査法^[4]やマイクロエンドミル等、微細加工工具先端の高感度位置センシング法^[5,6]へ適用した事例、加工メカニズムの解析評価技術としてCMPプロセスのスラリー挙動観察法^[7]へ適用した事例等が挙げられる。また計測評価技術に留まらず、エバネッセント光を直接、加工技術のエネルギーとして用いるナノ光造形法^[8]等の開発も進められている。

外部リンク

• 東京大学高橋道畑研究室

引用

1. R. C. Reddick : New form of scanning optical microscopy, Phys. Rev. B39, 1(1989)767.
2. P. A. Temple : Total internal reflection microscopy, Appl. Opt. 20, 15(1981)2656.
3. D. Axelrod : Total internal reflection fluorescence microscopy, Method Cell Biol. 30(1989) 245.
4. 吉岡淑江他：輪帯エバネッセント照明による回路パターン付きSiウエハの表面異物欠陥検出法に関する研究(第1報)－欠陥検出原理とその検証実験－，精密工学会誌，72, 7(2006)878.
5. 横尾一将他，：マイクロエンドミルによるガラスの切削加工－工具先端位置センシングおよび切削液の化学的影響－”，2006年度精密工学会春季大会学術講演会講演論文集, (2006)1029.
6. 谷川涼一他，：エバネッセント光を用いた工具-工作物間距離の直接計測，日本機械学会第9回生産加工・工作機械部門講演会講演論文集，10(2012)219
7. 出井良和他：エバネッセント場を用いたCMPプロセスでの研磨微粒子の挙動の観察, 日本機械学会関東支部第17期総会講演会講演論文集, 3(2011)571
8. 梶原優介他：エバネッセント光を利用したナノ光造形法に関する研究(第1報)－造形基本特性の理論的・実験的検討－，精密工学会誌，72, 11(2006)1396.

執　筆 ： 高橋　哲