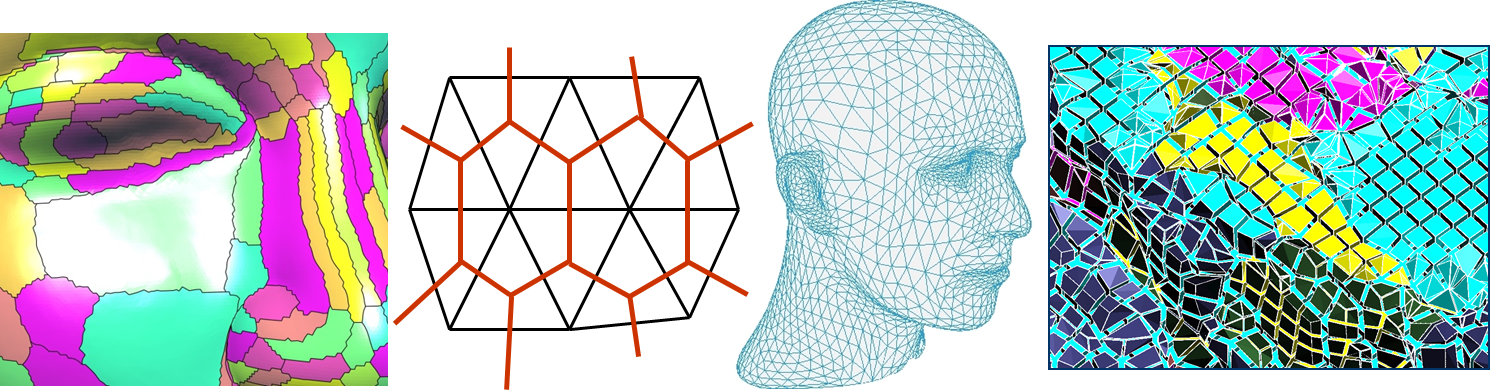
メッシュ処理 ( Mesh Processing ) とは、幾何形状・領域を一次近似・表現するポリトープ ( polytope ) 網を計算処理する事である。ここでポリトープとは、一般化された図形であり、例えば零次元から三次元までのポリトープはそれぞれ、点、線分、多角形、多面体である。メッシュはポリトープの和集合として与えられる。メッシュ処理では、幾何学全般に基づき幾何的又は位相的な操作を行う事で、新たなメッシュや多様体を生成する。また、メッシュ自体の幾何・位相情報の解析、誤差解析や物理計算の為にメッシュ情報の参照を行う事もメッシュ処理である。古代では多角形・多面体幾何学、近代では設計・近似のためのスプラインやボロノイ図等の研究がされているが、コンピュータの登場により、精密工学に密接なCAD・CAM・CAE・CAT及びCG・CVでの応用が盛んである。
- 基礎
- メッシュ処理に有用・必要な学問
- 処理の種類
- メッシュ化 ( meshing )
- 再メッシュ化 ( remeshing )
- 細分割 ( subdivision )
- 簡略化 ( simplification/decimation )
- 多重解像度・スペクトラム解析 ( multiresolutional/spectrum analyses )
- 関数近似・陰関数化・補間・意匠設計 ( fitting/implicitization/interpolation/aesthetic design )
- 平滑化・ノイズ除去 ( smoothing/noise reduction )
- 変形 ( deformation/warping )
- 位置合わせ ( registration )
- 圧縮・電子透かし ( compression/watermarking )
- 領域分割・カット ( segmentation/cutting )
- 媒介変数化 ( parameterization/flattening )
- 検索 ( retrieval )
- 特徴抽出(feature extraction)
- 測地線・測地距離 ( geodesics )
- 衝突・内外判定 ( collision detection )
- 国際会議・論文誌
- 関連項目
- 外部リンク
- 引用
基礎
メッシュはポリトープの集合であり、メッシュ処理とは、メッシュの幾何・位相情報を参照・追加・削除・変更する処理である。
メッシュ ( mesh )
ポリトープの集合。例えば、三角形メッシュ ( triangle mesh ) は、三角形の連結した集合である。多様体の一次近似又は曲線や曲面などの領域・空間を充足するダイアグラム ( diagram ) として用いる事が多いが、一般のグラフやデジタル画像なども広義のメッシュである。非多様体のメッシュとしては一部の単体的複体 ( simplical complex ) やCW-complex(中心軸:Medial Axis等)などがある。
ポリトープ ( polytope )
多角形や多面体等を一般化した幾何要素であり、n次元ポリトープは、ファセット ( facet ) やセル ( cell ) と呼ばれる(n-1)次元までのポリトープで構成される。零次元から三次元までのポリトープはそれぞれ、点、線分、多角形、多面体である。例えば、三角形は、3つの0-cellである頂点 ( vertex ) 、3つの1-cellである辺 ( edge ) 及び1つの2-cellである面 ( face ) から構成される。
k-近傍 ( k-ring、k-link )
頂点に辺で繋がったk番目の近傍。
Valence
頂点に繋がっている辺数。
Degree
面を構成している頂点数。
Connectivity
辺の繋がり情報。
メッシュの状態
多様体メッシュ ( manifold mesh )
1-linkがtopological disk(高次元ではball)と同位相である頂点のみで構成されたメッシュ。境界ではhalf-diskと同位相。曲面メッシュ ( surface mesh ) で最も用いられているのは多様体である三角形メッシュである。これは、どの様な位相の曲面でも三角形分割が可能である事と三角形メッシュの面は平面であり、法線ベクトルが一意に決まる事に起因する。また、物理計算やrenderingハードウェアでの三角形メッシュに基づく方法が非常に発達している事も三角形メッシュの普及に大きく寄与している。以後、特に断りがなければメッシュは多様体であることを仮定する。
n-連結メッシュ ( n-connected mesh )
任意のn個の頂点を削除しても連結しているメッシュ。
水密 ( watertight ) メッシュ
穴が無いメッシュ。例えば三角形メッシュでは、全ての辺が二つの三角形に共有されているメッシュ。
規則 ( Regular ) メッシュ
多角形のdegreeによってvalenceがメッシュ全体の全ての内部頂点で一定のメッシュ。例えば、三角形メッシュは内部頂点でvalenceが6、四角形メッシュは内部頂点でvalenceが4のメッシュ。重要な注意点としては、形状の位相によっては、regular meshがオイラー数の関係より、数学的に存在しない事である。従って大部分の頂点でregularなvalenceを満たすメッシュを準規則メッシュ ( semi-regular mesh ) と呼び、regularでない頂点をextraordinary vertexと呼ぶ。
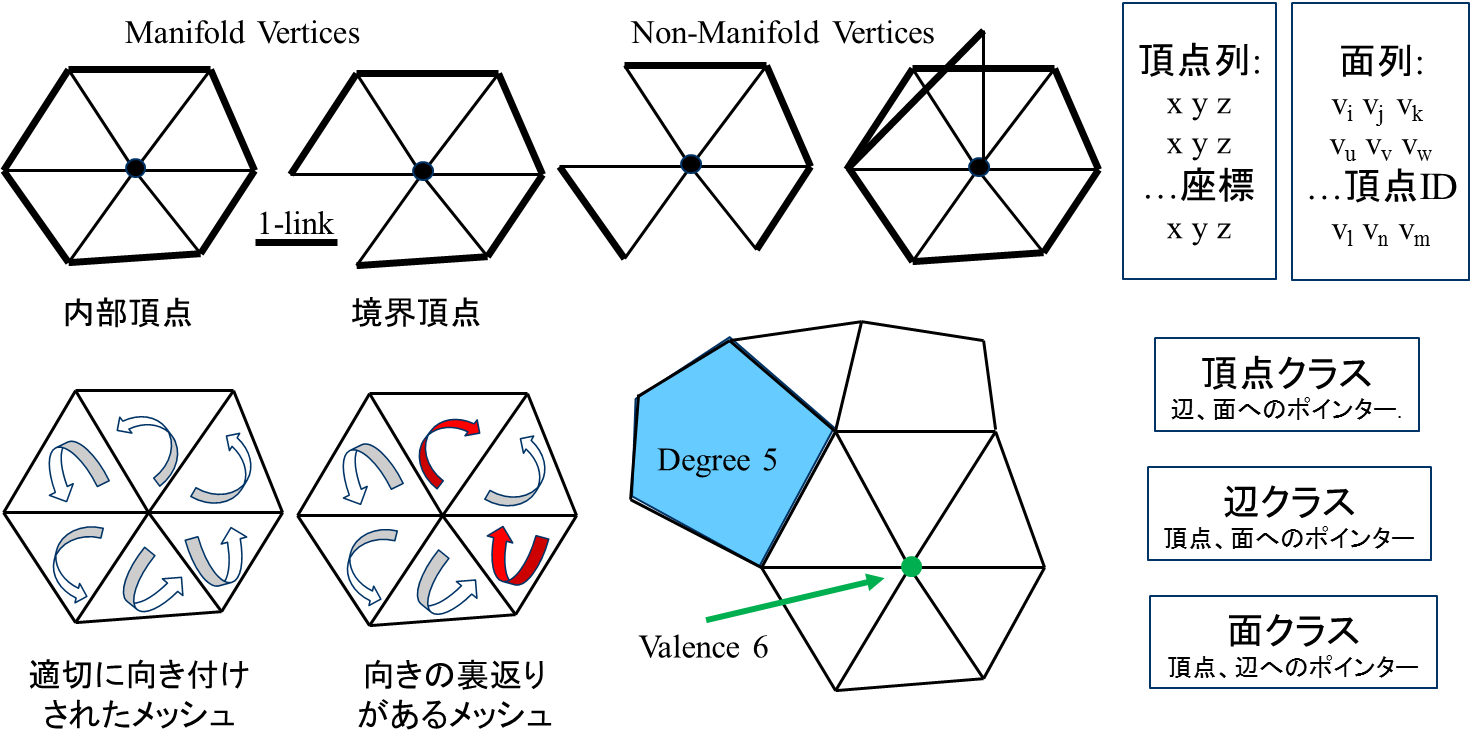
向き付け ( oriented ) メッシュ
全てのセルの方向が揃っているメッシュ。例えば三角形メッシュでは、三角形の頂点IDの並び順が右(又は左)周りで統一されたメッシュである。向き付けされたメッシュでは、三角形の法線ベクトルを導出する場合に、二つの辺の外積を統一した順番で計算するとメッシュ全体で揃った向きの法線が得られ、曲面の向きとなる。
データ構造
最も簡単なデータ構造は、次元毎にポリトープを多次元(又は複数やオブジェクト指向型言語でのクラスの)配列等に格納する方法である。例えば、三角形メッシュであれば面に基づくデータ構造が簡単で、頂点ID順に頂点位置を格納した頂点列と、頂点IDを三つ組みである面を面ID順に格納した面列で表現できる。このとき、向き付けされたメッシュの場合は、頂点IDの並び順を入れ替えない注意が必要である。
セルに基づくデータ構造
各セル毎に構造体やオブジェクト指向言語のクラスを用いてセルを定義し、その関係性を構造体・クラスのメンバー変数やポインターとして持つ構造もよく用いられている。例えば三角形メッシュであれば、頂点、辺、面毎にクラスを作成し、それぞれにポインターや変数で参照を行う ( half ) edgeデータ構造[1]が有名である。また、progressive mesh[2]等のメッシュの粗密階層を表現するデータ構造もある。
ファイルフォーマット
様々な種類があり、曲面メッシュではoff、ply、obj、stl等が有名である。最も簡単なascii offファイルフォーマットは、asciiテキストにて、一行目に「OFF」という文字列、二行目に頂点数、面数、辺数をスペース区切、三行目から頂点の3次元座標をスペース区切(一行一頂点)、頂点情報の後に面の頂点IDを一面一行毎にスペース区切で並べるだけである(頂点IDはゼロから始まる)。
STL(STereoLithography)の注意点
stlは様々なCAD/CAEソフトウェアで読み込みが可能な曲面メッシュで幅広く用いられている。ファイルフォーマット名であり、メッシュ自体の呼称ではない。幾何学的な注意点として、頂点を面毎に重複して持つため、データ量が多くなるだけではなく、同一頂点である事に一意性が無い。offやobjフォーマットなどは、その様な曖昧さを回避出来るだけではなく、重複頂点も表せる。
応用
幅広い分野で様々な目的にメッシュ処理は用いられている。特に、CG ( Computer Graphics )、CAD ( Computer Aided Design )、CV ( Computer Vision )、及び計算物理学/CAE ( Computational Physics/Computer Aided Engineering ) での形状・計算領域の表現にて重要である。
メッシュ処理に有用・必要な学問
メッシュ処理は幾何学全般に基づいており、数学モデル・定理、離散化やアルゴリズムなど幅広い数学的・情報学的な知識が必要である。
微分幾何学
※ 引用[3,4]参照
メッシュを多様体の近似として用いる場合に、長さや曲率などの計量を考えるのに必要である。
位相幾何学
※ 引用[5,6]参照
穴やハンドル ( topological handle ) の数などメッシュの繋がり具合を考える場合に必要。多様体を近似しているメッシュだけでなく、有名なオイラー数 ( Euler Characteristics ) や種数 ( genus ) などメッシュ自体の位相構造でも重要である。
計算幾何学/組合せ幾何学/多面体幾何学
※ 引用[7-10]参照
ボロノイ図 ( Voronoi diagram ) やその双対 ( dual ) であるドロネー図(Delaunay三角形分割)の構成方法や幾何構造の組合せ・配置に関する数学。
曲線と曲面の幾何学/スプライン
※ 引用[11-13]参照
メッシュを曲線・曲面の近似として用いる場合に必要である。また、スプライン ( spline ) の制御メッシュなど空間を定義するのに用いる。
グラフ理論
※ 引用[14]参照
媒介変数化 ( mesh parameterization ) でのグラフの埋め込みやグラフラプラス作用素の固有値解析などメッシュ構造自体の解析に有用である。また、EMST ( Euclidean minimum spanning tree ) やGabriel/Reebグラフなどは点群のメッシュ化、曲面メッシュの分割、メッシュのスケルトン(アニメーションや変形のための中心構造)抽出にて有用である。
アルゴリズムとデータ構造
※ 引用[15]参照
通常、メッシュの要素数は大きいため、メッシュ構造の探索や並び替え等の基本操作にて効率的なデータ構造と計算方法が必要である。また、木構造の操作なども広義のメッシュ処理と言える。
近似理論・数値解析
※ 引用[16]参照
曲線や曲面の離散化、多元線形連立方程式や偏微分方程式の解法、最適化問題の解法などの数値解析はメッシュ処理で必要な技術である。
信号・画像処理
※ 引用[17]参照
離散化された一次元信号や画像は、メッシュの特殊な場合と考えられる。それゆえ、フィルタや多重解像度解析などの数理モデル・方法論を一般のメッシュ処理に拡張する場合に有用である。
処理の種類
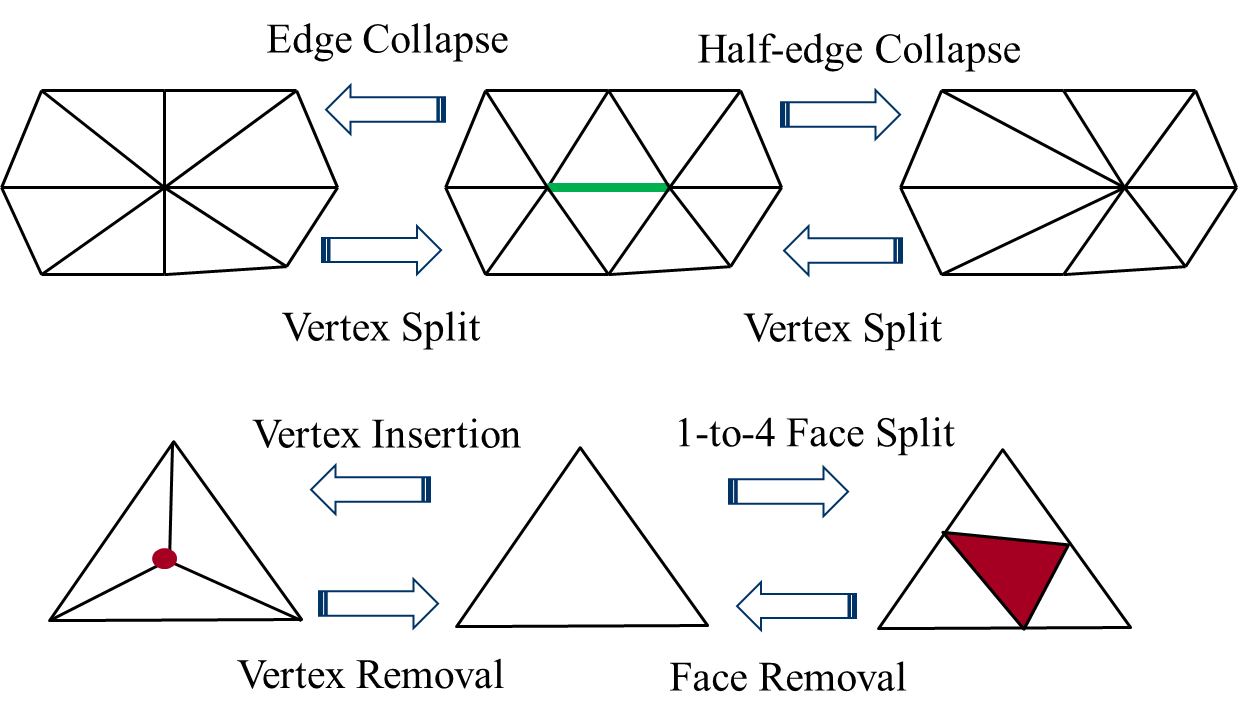
メッシュ処理には大別して、幾何・位相・局所・大域及びその組合せの処理がある。幾何及び位相の処理は、それぞれ頂点座標とconnectivityに対して行う処理である。局所的な処理(例えば図3の操作)は、メッシュ内の限定された領域にしか影響を及ぼさない(又は用いない)処理であり、大域的な処理はその逆である。形状や領域の近似精度、滑らかさ、ポリトープ要素の性質(例えば三角形の形など)を基準に処理を行う。具体的なメッシュ処理の目的や方法は非常に多様である。下記に代表的な処理の例を挙げる。
メッシュ化 ( meshing )
領域を充足する格子生成[18]や点群、スプライン、陰関数などからメッシュを構成する処理。特に曲面メッシュの場合は、曲面再構成問題[19,20]として知られる。また、陰関数からのメッシュ生成はMarching Cube法[21]が有名である。
再メッシュ化 ( remeshing )
与えられたメッシュをポリトープのサイズ、数、形状などが異なる性質をもつメッシュに変換する処理。例えば、有限要素解析では均一の大きさの正三角形が良いとされるが、形状近似では主曲率の比と主方向に沿った長細い三角形が最適である事が知られている[22]。また、二つ以上のメッシュの縫い合わせ ( stitching ) なども再メッシュ化の一種である。
細分割 ( subdivision )
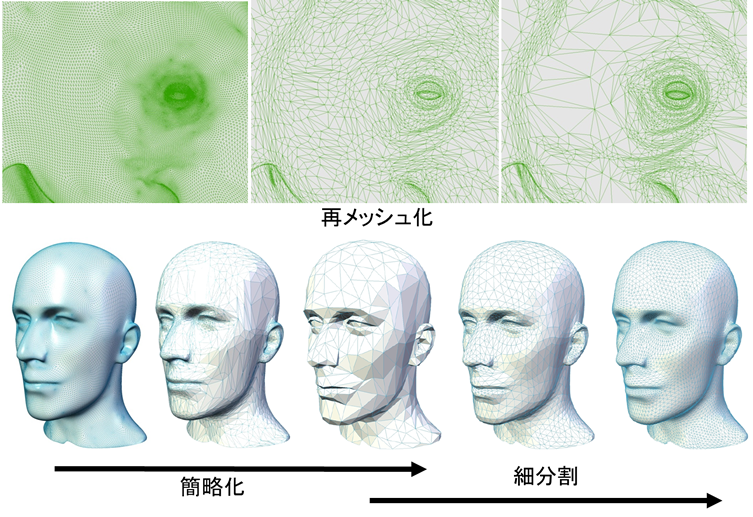
ポリトープを細かく分割する処理。ある規則に従って細分割を行うと、B-spline等の連続で滑らかなスプラインに収束する事が知られている[23]。Chaikin[24]やLoop[25]のアルゴリズムが有名であり、Wavelet等の多重解像度解析とも密接に関連している[23]。
簡略化 ( simplification/decimation )
元の形状を近似しながらポリトープの数を減らす処理[26]。QSlim[27]が非常に有名である。QSlimは、局所的な幾何・位相操作をpriority heap queueを用いて行うなど、メッシュ処理の基礎が詰まっている(Loopの細分割法[25]及び平均曲率流 ( mean curvature flow ) [28]と合わせて初学者の学習向けにも優れている)。
多重解像度・スペクトラム解析 ( multiresolutional/spectrum analyses )
メッシュを周波数分解・操作する処理.細分割と簡略化を用いてB-spline waveletの 拡張とする方法群[29]やメッシュのラプラス作用素の固有関数展開[30]等がある。周波数別に形状を操作する事で、詳細強調・平滑化・変形など様々な処理に有用である。
関数近似・陰関数化・補間・意匠設計 ( fitting/implicitization/interpolation/aesthetic design )
メッシュからベジエ/NURBS[11,12]等の連続で滑らかな多様体や離散近似としての意匠メッシュ(Euler スプライン、Willmore曲面、Thin-plate spline等)[31]の生成を行う処理。
平滑化・ノイズ除去 ( smoothing/noise reduction )

形状を平滑化し、ノイズの除去を行う処理。信号・画像処理のフィルタ理論が適応されているだけではなく、平均曲率流 ( mean curvature flow )[28,32]やScreened Poisson方程式[33]などの幾何学的な偏微分方程式に基づく方法群が多数提案されている。また、平滑化処理は、細分化、多重解像度解析、変形などで基礎操作として用いられている。
変形 ( deformation/warping )
形状を幾何学的に変形する処理。FFD ( Free-Form Deformation)[34]やRBF ( Radial Basis Function ) などを使用してメッシュが埋め込まれた空間を変形するアプローチ、力学変形を簡略化する方法群や、メッシュのラプラス作用素とPoisson方程式に基づく方法群[35,36]等がある。Poisson方程式に基づく方法群は、画像や形状のseamless合成へも適用されている。
位置合わせ ( registration )
複数のメッシュに対して、共通部分の位置を合わせる処理[37]。例えば、表面レーザースキャナーや車載の動画像から一致する位置を推定し、張り合わせるために行う。
圧縮・電子透かし ( compression/watermarking )
メッシュ情報をデータ量の削減(圧縮[38])や暗号化[39]を行う処理。単純なハフマン符号化以外にもメッシュの特性を生かした圧縮方法がある。
領域分割・カット ( segmentation/cutting )

メッシュの領域を分割する処理[40,41]。曲面メッシュの場合は、部分的に平面や代数曲面などの要素形状で近似できる様に分割する。重心ボロノイ図に基づく方法群や媒介変数化のための切り線生成 ( cutting ) などがある。
媒介変数化 ( parameterization/flattening )
二つのメッシュ間に写像を生成する処理[42-44]。特に曲面・volumeメッシュにおいて、一次元下の多様体への写像を生成する媒介変数化は、再メッシュ化やテクスチャーマッピングなどで有用である。通常は、位相が同じ又は異なる形状間の歪(角度、面積、長さなど微分幾何学で与えられる測度による基準)が少ない写像の構成を行う。
検索 ( retrieval )
データベースより、与えられた形状に近い形状を検索する処理[45,46]。画像処理・パターン認識の方法論が拡張・適応されている。
特徴抽出(feature extraction)
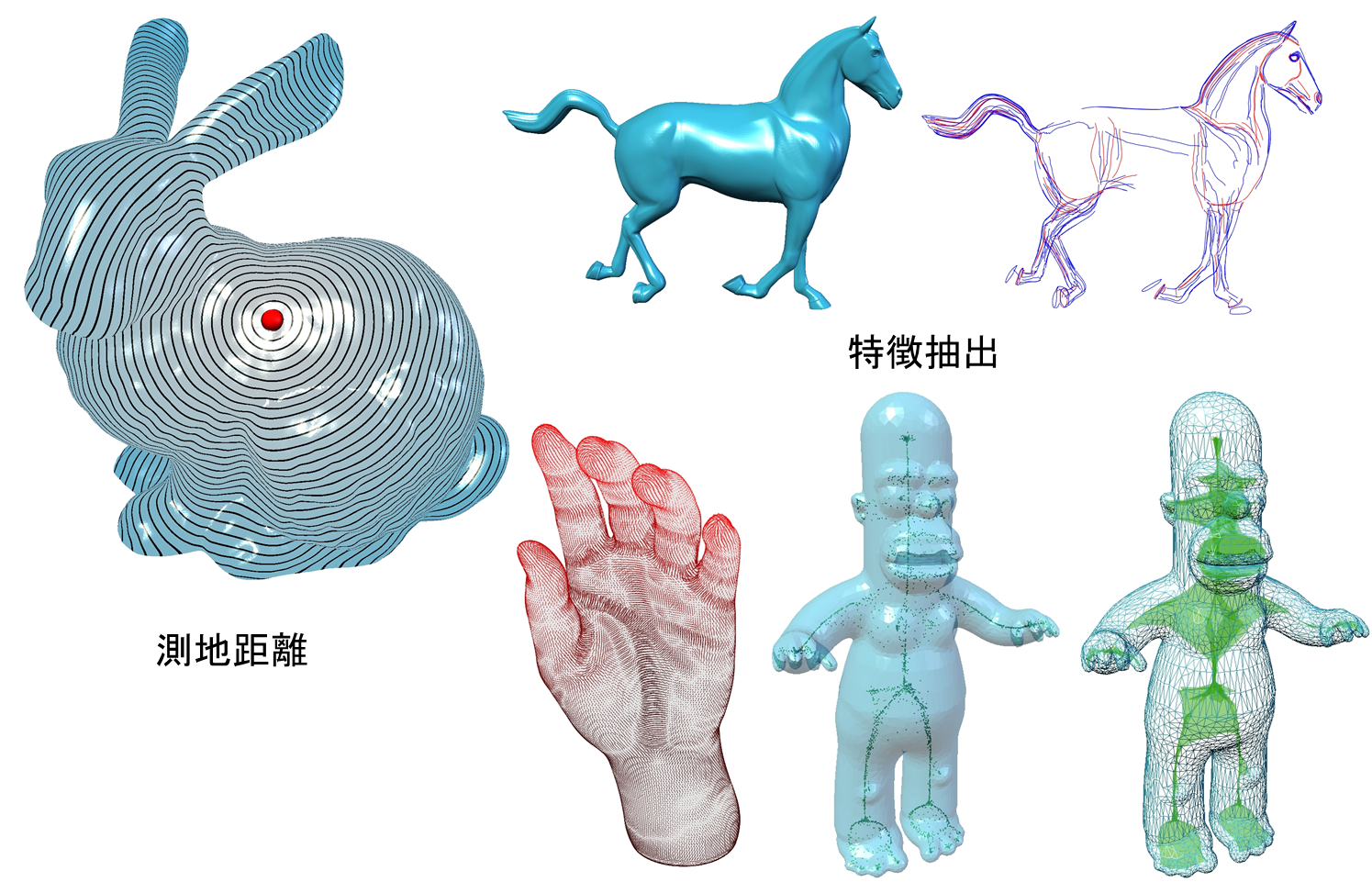
幾何・位相的な特徴を計算し抽出する処理。山尾根谷線 ( ridge-valley/crest curve )[47]などの曲面上の特徴線[12,48]、対象度合、滑らかさ、中心軸等の幾何特徴、オイラー数や種数などの位相特徴など多種多様な特徴抽出がある。また、形状検索に用いるパターン認識の特徴などもある。
測地線・測地距離 ( geodesics )
メッシュ上の二点を結ぶ最短距離・最短曲線である測地距離・測地線を計算する処理[49,50]。物理計算や形状モデリングにて様々な応用がある。
衝突・内外判定 ( collision detection )
複数メッシュの衝突・内外の判定を行う処理[51-53]。計算・組合せ幾何学[6-9]の方法群の他にも、Level-set[32]による判定方法もある。
国際会議・論文誌
SGP/SPM/SMIなどの幾何処理・形状モデリングの国際会議(Computer Scienceの国際会議は二段組み10頁前後の査読付きfull paperである事が多い)以外にも、メッシュ・格子生成のIMRや計算幾何学のACM SCGなどが有名である。さらにCG全般のSIGGRAPH/EG/PGやCV全般のICCV/CVPRでも質の高い学術論文が毎年発表されている。メッシュ処理に関する論文が多い国際会議・論文誌は多数あり、下記は一部である。
- 幾何処理・形状モデリング系の国際会議
SGP: Eurographics Symposium on Geometry Processing.
SPM: (ACM) Symposium on Solid and Physical Modeling.
SMI: (IEEE) International Conference on Shape Modeling and Applications (Shape Modeling International).
IMR: International Meshing Roundtable.
SCG: ACM Symposium on Computational Geometry.
GMP: International Conference on Geometric Modeling and Processing.
MoS: IMA Conference on Mathematics of Surfaces.
MMCS: International Conference on Mathematical Methods for Curves and Surfaces.
EG Workshop on 3D Object Retrieval. - CG/CV全般の国際会議
ACM SIGGRAPH: ACM International Conference and Exhibition on Computer Graphics and Interactive Techniques.
EG (Eurographics): Annual Conference of the European Association for Computer Graphics.
PG (Pacific Graphics): Pacific Conference on Computer Graphics and Applications.
GI (Graphic Interface): International Conference on Graphics, Visualization and Human-Computer Interaction.
CGI: Computer Graphics International.
VIS: IEEE Visualization Conference.
ICCV: IEEE International Conference on Computer Vision.
CVPR: IEEE Conference on Computer Vision and Pattern Recognition. - 学術論文誌
ACM TOG: ACM Transactions on Graphics.
CAGD: Computer Aided Geometric Design.
CAD: Computer Aided Design.
CGF: Computer Graphics Forum.
The Visual Computer.
Graphical Models.
TVCG: IEEE Transactions on Visualization and Computer Graphics.
TPAMI: IEEE Transactions on Pattern Analysis and Machine Intelligence.
IJCV: International Journal of Computer Vision.
Journal of Computational Physics.
関連項目
外部リンク
- 東京大学 鈴木・大竹研
- 東京大学 金井研
- カルフォルニア工科大学Caltech Multi-Res Modeling Group: Dr. Peter Schroder
- マイクロソフト研究所: Dr. Hugues Hoppe
- アーヘン工科大学 Computer Graphics and Multimedia: Dr. Leif Kobbelt
- フランス国立情報学自動制御研究所 INRIA: Dr. Pierre Alliez
- フランス国立情報学自動制御研究所 INRIA: Dr. Jean-Daniel Boissonnat
- カルファルニア大学バークリー校: Dr. Jonathan Shewchuk
- オーストリア科学技術研究所: Dr. Herbert Edelsbrunner
- NVIDIA研究所: Dr. Michael Garland
- カルフォルニア大学デイビス校: Dr. Nina Amenta
- ウィーン工科大: Dr. Helmut Pottman
- テルアビブ大学: Dr. Daniel Cohen-Or
- イスラエル工科大: Dr. Craig Gotsman
- オスロ大学: Dr. Michael Floater
- グルノーブル理工大学: Dr. Marie-Paule Cani
- ハーバード大学: Dr. Steven Gortler
- ベルリン自由大学: Dr. Konrad Polthier
- ブリティッシュコロンビア大学: Dr. Alla Sheffer
- ニューヨーク大学: Dr. Denis Zorin
- カーディフ大学: Dr. Ralph Martin
- トロント大学: Dr. Karan Singh
- ブラウン大学: Dr. Gabriel Taubin
- スイス連邦工科大学ローザンヌ校: Dr. Mark Pauly
- ベルリン工科大学: Dr. Marc Alexa
- スイス連邦工科大学チューリッヒ校: Dr. Olga Sorkine
- ワシントン大学: Dr. Tao Ju
- ルガーノ大学: Dr. Kai Hormann
- ジョージア工科大 Computer Graphics Group
- マックスプランク・コンピュータ科学研究所
- Solid Modeling Association
引用
- M. Botsch, L. Kobbelt , M. Pauly , P. Alliez, and B. Levy, “Polygon Mesh Processing”, A K Peters/CRC Press, 2011.
- H. Hoppe, “Progressive Meshes”, Proc. ACM SIGGRAPH, pp. 99-108, 1996.
- D. Struik, “Lectures on Classical Differential Geometry”, Dover Publications, 1988.
- E. Abbena , A. Gray, and S. Salamon, “Modern Differential Geometry of Curves and Surfaces with Mathematica, 4th Ed”, Chapman and Hall/CRC, 2016.
- 前原 濶, “直観トポロジー”, 共立出版, 1993.
- A. Fomenko and T. Kunii, “Topological Modeling for Visualization”, Springer, 2013.
- H. Edelsbrunner, “Algorithms in Combinatorial Geometry”, Springer-Verlag, 1987.
- 杉原 厚吉, “計算幾何学”, 朝倉書店, 2013.
- 今井 浩, 今井 桂子, “計算幾何学”, 共立出版, 1994.
- P. R. クロムウェル (著), 下川航也 (訳), 平澤美可三 (訳), 松本三郎 (訳), 丸本嘉彦 (訳), 村上斉 (訳), “多面体”, 数学書房, 2014.
- G. Farin, “Curves and Surfaces for CAGD, Fifth Edition: A Practical Guide”, Morgan Kaufmann, 2001.
- 穂坂 衛(著), 東 正毅 (訳), 久志本 琢也 (訳), 斉藤 剛 (訳), “CAD/CAMにおける曲線曲面のモデリング”, 東京電機大学出版局, 1996.
- J. Koenderink, “Solid Shape”, MIT Press 1990.
- W. Tutte, “Graph Theory”, Cambridge University Press, 2001.
- R. Sedgewick, “Algorithms in C, Parts 1-5 (Bundle): Fundamentals, Data Structures, Sorting, Searching, and Graph Algorithms”, Addison-Wesley Professional, 2001.
- W. Press, S. Teukolsky, W. Vetterling, and B. Flannery, “Numerical Recipes: The Art of Scientific Computing 3rd Edition”, Cambridge University Press, 2007.
- R. Gonzalez, “Digital Image Processing”, Prentice Hall; 3rd edition, 2007.
- Joe F. Thompson (編), Bharat K. Soni (編), Nigel P. Weatherill (編) , “Handbook of Grid Generation”, CRC Press, 1998.
- 大竹 豊, “点群からの表面再構成”, 計算工学 16(2), pp. 2523-2527, 2011.
- 長井 超慧, “3Dスキャナによる計算機への現物形状入力”, 精密工学会誌 79(6), pp. 497-501, 2013.
- W. Lorensen and H. Cline, “Marching cubes: A high resolution 3D surface construction algorithm”, Proc. ACM SIGGRAPH, pp. 163-169, 1987.
- P. Alliez, M. Attene, C. Gotsman, and G. Ucelli, “Recent Advances in Remeshing of Surfaces”, Shape Analysis and Structuring, pp. 53-82 , 2007.
- D. Zorin, P. Schroeder, T. DeRose, L. Kobbelt, A. Levin, and W. Sweldens, “Subdivision for Modeling and Animation”, ACM SIGGRAPH courses, 2000.
- G. Chaikin, “An Algorithm for High Speed Curve Generation”, Computer Graphics Image Processing, 3(12), pp. 346-349 , 1974.
- C. Loop, “Smooth Subdivision Surfaces Based on Triangles”, M.S. Mathematics thesis, University of Utah, 1987.
- M. Garland, “Quadric-Based Polygonal Surface Simplification”, PhD Dissertation, Carnegie Mellon University, 1999.
- M. Garland and P. Heckbert, “Surface simplification using quadric error metrics”, Proc. ACM SIGGRAPH, pp. 209-216, 1997.
- M. Desbrun, M. Meyer, P. Schroder, and A. Barr, “Implicit fairing of irregular meshes using diffusion and curvature flow”, Proc. ACM SIGGRAPH, pp. 317-324, 1999.
- P. Heckbert, J. Rossignac, H. Hoppe, W. Schroeder, M. Soucy, and A. Varshney, “Multiresolution Surface Modeling”, ACM SIGGRAPH courses, 1997.
- B. Levy and H. Zhang, “Spectral mesh processing”, ACM SIGGRAPH courses, 2010.
- E. Grinspun, M. Desbrun, K. Polthier, P. Schroder, and A. Stern, “Discrete Differential Geometry: An Applied Introduction”, ACM SIGGRAPH courses, 2007.
- J. Sethian, “Level Set Methods and Fast Marching Methods”, 2nd edition, Cambridge University Press, 1999.
- M. Chuang and M. Kazhdan, “Interactive and anisotropic geometry processing using the screened Poisson equation”, ACM TOG (SIGGRAPH), 30(4), pp. 57:1–57:10, 2011.
- T. Sederberg and S. Parry, “Free-form deformation of solid geometric models”, Proc. ACM SIGGRAPH, pp. 151-160, 1986.
- O. Sorkine, “Laplacian Mesh Processing”, EUROGRAPHICS STAR, 2005.
- M. Alexa, “Mesh editing based on discrete Laplace and Poisson models”, ACM SIGGRAPH courses, 2006.
- F. Bogo, J. Romero, M. Loper, and M. Black, “FAUST: Dataset and Evaluation for 3D Mesh Registration”, Proc. IEEE CVPR, pp. 3794 – 3801, 2014.
- P. Alliez and C. Gotsman, “Recent Advances in Compression of 3D Meshes”, Advances in Multiresolution for Geometric Modelling, pp 3-26, 2004.
- K. Wang, G. Lavoue, F. Denis, and A. Baskurt, “Three-dimensional meshes watermarking: review and attack-centric investigation”, Proc. International Conference on Information Hiding, pp. 50-64, 2007.
- A. Shamir, “A survey of mesh segmentation”, Computer Graphics Forum, 27(6), pp. 1539-1556, 2008.
- H. Benhabiles , J.-P. Vandeborre, G. Lavoue, and M. Daoudi, “A comparative study of existing metrics for 3D-mesh segmentation evaluation”, The Visual Computer, 26(12), pp. 1451-1466, 2010.
- M. Floater and K. Hormann, “Surface Parameterization: a Tutorial and Survey”, Advances in Multiresolution for Geometric Modelling, pp. 157-186, 2005.
- A. Sheffer, E. Praun, and K. Rose, “Mesh parameterization methods and their applications”, Found. Trends. Comput. Graph. Vis., 2(2), pp. 105-171, 2006.
- K. Hormann, B. Levy, and A. Sheffer, “Mesh parameterization: theory and practice”, ACM SIGGRAPH courses, 2007.
- A. Bronstein, M. Bronstein, M. Ovsjanikov, and L. Guibas, “Shape Google: geometric words and expressions for invariant shape retrieval”, ACM TOG, 30(1), pp. 1-20, 2011.
- E. Boyer et al., “SHREC 2011: robust feature detection and description benchmark”, Proc. EG Workshop on 3D Object Retrieval, pp. 71-78, 2011.
- S. Yoshizawa, A. Belyaev, H. Yokota, and H.-P. Seidel, “Fast, Robust, and Faithful Methods for Detecting Crest Lines on Meshes”, CAGD, 25(8), pp. 545-560, 2008.
- S. Rusinkiewicz, F. Cole, D. DeCarlo, and A. Finkelstein, “Line Drawings from 3D Models”, SIGGRAPH Asia class, 2008.
- V. Surazhsky, T. Surazhsky, D. Kirsanov, S. Gortler, and H. Hoppe, “Fast exact and approximate geodesics on meshes”, ACM TOG (SIGGRAPH), 23(3), pp. 553-560, 2005.
- K. Crane, C. Weischedel, and M. Wardetzky, “Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow”, ACM TOG, 32(5), pp. 152:1-152:11, 2013.
- B. Mirtich, “V-Clip: fast and robust polyhedral collision detection”, ACM TOG, 17(3), pp. 177-208, 1998.
- F. Madera, “An Introduction to the Collision Detection Algorithms”, Abstraction & Application, 5, pp. 7-18, 2011.
- M. Muller, N. Chentanez, T.-Y. Kim, and M. Macklin, “Air meshes for robust collision handling”, SCM TOG (SIGGRAPH), 34(4), pp. 133:1-133:9, 2015.
執 筆 : 吉澤 信
