ループ剛性 ( Loop stiffness ) とは、工具-工作機械-工作物で構成される力学的閉ループ構造の剛性である。主に工具-工作物間のループ剛性 ( Tool-workpiece loop stiffness ) のことを指す。
詳細
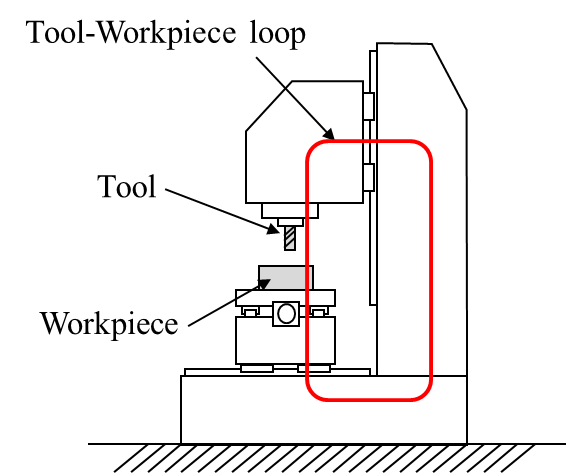
機械加工において、加工力および加工反力は作用反作用の法則によって工具と工作物に同時に作用し、両者の間に相対変位を生じさせる。このとき、加工反力は工具-工作機械-工作物で構成される力学的閉ループ(図1)に作用し、相対変位の大きさはこのループの剛性に依存する。
ループ剛性の評価方法
通常、ループ剛性は逆数であるループコンプライアンス ( Loop compliance )によって評価される。さらに、加工反力は周期成分を持つため、周波数応答関数 ( Frequency response function : FRF ) として、動コンプライアンス ( Dynamic compliance ) を評価する。
加工反力と工具-工作物間の相対変位の関係は次式で表される。
\( \begin{pmatrix} D_x\\D_y\\D_z\\ \end{pmatrix} = \begin{pmatrix} G_{xx} G_{xy} G_{xz}\\G_{yx} G_{yy} G_{yz}\\G_{zx} G_{zy} G_{zz}\\ \end{pmatrix} \begin{pmatrix} F_x\\F_y\\F_z\\ \end{pmatrix} \) (1)
ここで、\(D_x\)、\(D_y\)、\(D_z\) は工具-工作物間の相対変位、\(G_{ij}\)は\(j\)方向の加工反力で生じた\(i\)方向の変位に関するコンプライアンス、\(F_x\),\(F_y\),\(F_z\)は加工反力である。コンプライアンスマトリクスにおける対角項\( G_{ij}(i=j) \)をダイレクトコンプライアンス ( Direct compliance ) 、非対角項\( G_{ij}(i \neq j) \)をクロスコンプライアンス ( Cross compliance ) と呼ぶ。
ループコンプライアンスの測定では、工具と工作物を加振し、加振力と工具-工作物間の相対変位を測定する必要がある。一般的には、加振方法の異なる以下の3つの方法が用いられる。
(1)加振器を用いる方法[1,2]
工具と工作物との間に圧電素子などによる加振器を設置し、工具―工作物間ループを加振する。加振力パターンの自由度が高く、周波数帯域を自由に設定することができるが、付加的な装置として加振器が必要である。
(2)切削反力を用いる方法[3]
切削反力によって工具と工作物を加振する。断続切削によって衝撃的な加振力を発生させ、広い周波数帯域での加振を実現する。プロセスダンピングなど、切削メカニズムに起因する動特性を含めて、実加工状態に近いループコンプライアンスを評価できる一方、周波数帯域の自由度が低い。
(3)インパクト試験による方法
ハンマと加速度計を用いた一般的なインパクト試験によっても、簡易的にループコンプライアンスを求めることができる。工具と工作物の自己コンプライアンスを測定し、コンプライアンスの差をとることで、ループコンプライアンスを求める。インパクト試験によって比較的手軽に評価が行えるが、加振力の作用する部分が工具-工作物間のループと厳密には一致しない。
ループ剛性の位置依存性と方向依存性
ループ剛性はワークスペース内における位置と加振力の方向によって変化する。位置依存性に関しては、ワークスペース内の複数の位置でのループ剛性に基づいて、プロセスの安定性を評価する方法がある[4,5]。方向依存性に関しては、式(1)におけるコンプライアンスマトリクスを求めることが出来れば、2階のテンソルの回転によって、任意の方向のコンプライアンスを求めることができる[1]。
引用
- D. Kono and A. Matsubara, Investigation of direction dependency of tool-workpiece compliance of machine tool, Procedia CIRP 46 (2016) 529-532, open access.
- D. Kono, Y. Moriya, A. Matsubara, Influence of rotary axis on tool-workpiece loop compliance for five-axis machine tools, Precision Engineering, 49 (2017), 278–286.
- N. Tounsi and A. Otho, Identification of machine–tool–workpiece system dynamics, International Journal of Machine Tools & Manufacture 40 (2000) 1367–1384.
- M. Law, Y. Altintas and A. S. Phani, Rapid evaluation and optimization of machine tools with position-dependent stability, International Journal of Machine Tools & Manufacture 68 (2013) 81-90.
- J. J. Zulaika, F. J. Campa, L. N. Lopez de Lacalle, An integrated process–machine approach for designing productive and light weight milling machines, International Journal of Machine Tools & Manufacture 51 (2011) 591-604.
執 筆 : 河野 大輔