トポロジー最適化
トポロジー最適化 ( topology optimization ) とは、数学的・力学的根拠に基づき、構造物の最適な形状と形態を求める方法論である。
目次 |
詳細
基礎理論
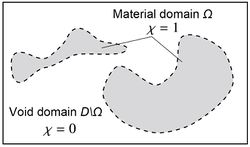
トポロジー最適化の基本的な考え方は,対象とする設計領域Ωを包含する固定された設計領域(固定設計領域)Dと,次式の特性関数χの導入にある[1][2][3].
ここで,xは固定設計領域における任意の位置座標を表す.特性関数χは固定設計領域Dにおける材料の有無を表していることから,χに関する最適化問題を考えると,トポロジー最適化は固定設計領域における材料分布問題に帰着される.これにより,固定設計領域において任意の形状と形態を表現することができる(図1).
設計空間の緩和
特性関数は可積分性のみが保証された不連続関数であることから,固定設計領域の至る所において無限小の空隙が存在するような構造をも最適解として許容する.そのため,大域的な意味でこの不連続問題を連続問題に置き換える緩和法として均質化法や密度法等が用いられている[2][3].これらの方法に基づくトポロジー最適化では,特性関数を連続的に変化する正規化された密度に対応させることで,固定設計領域における材料分布を表現する.したがって,中間的な材料密度を有する領域(グレースケール)を最適構造として許容することから,工学的に意味を持つ最適構造を得るためには,フィルタリング等を用いることによって材料分布の二値化を行いながら最適化を実行する必要性がある.他方,本質的にグレースケールを含まずに明確な境界を有する最適構造を得る方法として,レベルセット法に基づくトポロジー最適化が提案されている[4].
数値実装
殆どの場合において,対象とする物理場や材料分布は有限要素法によって離散化される.また,設計変数は離散化された各要素の材料密度に対応することから,トポロジー最適化では多くの設計変数を扱う必要がある.そのため,設計感度の算出には設計変数の数に依存しない感度解析手法である随伴変数法が通常用いられる.また,設計変数の更新方法としては,最適性基準法,逐次線形計画法,逐次凸関数近似法等が通常用いられる[2][3].
適用例
図2に示すように,左端を固定し,右下端に荷重を付加した片持ち梁を考える.ここでは片持ち梁の体積を固定設計領域の40%以下とする制約条件を与えた上で,構造物の剛性を最大化することを目的としている.密度法に基づくトポロジー最適化によって得られた最適構造を図3に示す.剛性最大化問題はトポロジー最適化のベンチマークとして用いられることが多い.
応用展開
熱,流体,電磁波等の構造力学以外を対象とした物理場,ならびにこれらの物理場を同時に考慮した連成問題への展開についても盛んに研究が行われている[2][3].また,付加製造技術との相性が良いことから,製造性を考慮した方法等についても研究が行われている[5].
外部リンク
引用
- ↑ M.P. Bendsøe and N. Kikuchi, Generating optimal topologies in structural design using a homogenization method, Computer Methods in Applied Mechanics and Engineering, Vol. 74, No. 2, pp.197-224, 1988.
- ↑ 2.0 2.1 2.2 2.3 M.P. Bendsøe and O. Sigmund, Topology optimization: theory, methods and applications, Springer, New York, 2003.
- ↑ 3.0 3.1 3.2 3.3 西脇眞二,泉井一浩,菊池昇,トポロジー最適化,日本計算工学会編,丸善,2013.
- ↑ N.P. van Dijk, K. Maute, M. Langelaar and F. van Keulen, Level-set methods for structural topology optimization: a review, Structural and Multidisciplinary Optimization, Vol. 48, No. 3, pp.437-472, 2013.
- ↑ T. Zegard and G.H. Paulino, Bridging topology optimization and additive manufacturing, Structural and Multidisciplinary Optimization, Vol. 53, No. 1, pp.175-192, 2016.