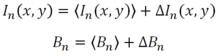「ゴーストイメージング」の版間の差分

提供: Precipedia
移動: 案内、 検索
(ページの作成:「<b>ゴーストイメージング </b> ( Ghost Imaging ) 2次元撮像デバイス（例えば，CCD素子）を用いることなく、空間的に分解能を持たな...」)
 
1行: 1行:
−
<b>ゴーストイメージング </b> ( Ghost Imaging ) 2次元撮像デバイス（例えば，CCD素子）を用いることなく、空間的に分解能を持たない点型光検出器（例えば，フォトダイオード）を用いてイメージングする手法であり、ランダムな光強度分布を持つ照明光と被撮影物体との強度相関を利用することで高感度なイメージングを実現する手法である。
+
<b>ゴーストイメージング </b> ( Ghost Imaging )とは， 2次元撮像デバイス（例えば，CCD素子）を用いることなく、空間的に分解能を持たない点型光検出器（例えば，フォトダイオード）を用いてイメージングする手法であり，ランダムな光強度分布を持つ照明光と被撮影物体との強度相関を利用することで高感度なイメージングを実現する手法である．
  
 
==詳細==
 
==詳細==

2017年1月27日 (金) 17:56時点における版

ゴーストイメージング ( Ghost Imaging )とは， 2次元撮像デバイス（例えば，CCD素子）を用いることなく、空間的に分解能を持たない点型光検出器（例えば，フォトダイオード）を用いてイメージングする手法であり，ランダムな光強度分布を持つ照明光と被撮影物体との強度相関を利用することで高感度なイメージングを実現する手法である．

目次

詳細

歴史

　ゴーストイメージングは，1995年にPittmanらにより初めて報告があった[1] (前年のBelinskyらの報告を第１報とする説もある[2])．なお，“ゴースト”という単語の使用は，同年に同じ研究グループが発表した論文でオーソライズされている[3]．当初は，量子論に関する実験に利用されており，特に，光子対の空間的なもつれの実証に用いられていた[4]．その後，光源を回転すりガラスに光照射することで発生するスペックルパターンに置き換えた，古典論的ゴーストイメージングが提案された[5][6][7][8]．また，MITのShapiroが，照明光強度分布を伝搬計算より求めた計算機ゴーストイメージングを発表した[9]．なお，その際に，Physical Review誌上で古典論的立場と量子論的立場でのゴーストイメージングに関する論争が巻き起こったのは興味深い．さらにその後，光源にプロジェクタを用いる計算機ゴーストイメージングが提案され，簡単な光学系で実現できるようになり，普及することとなった．

原理 〜揺らぎの２次相関分布〜

図1 ゴーストイメージングの原理

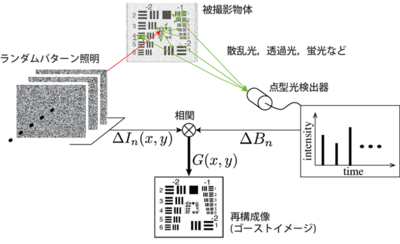
　図１に，ゴーストイメージングの原理を示す．撮影したいサンプルに対してランダムな光強度分布を持つ照明光を複数回照明する．各照明において，サンプルと作用した光（散乱，透過や蛍光など）を点型光検出器で光強度を取得する．ことのとき，n 回目に照明した光強度分布 In(x, y) および検出光強度 Bn は，それぞれ，

Ghost imaging eq01.png

と表すことができる．ここで，〈　〉および ∆ は，アンサンブル平均および揺らぎ（平均値からの偏差）をそれぞれ意味する．このとき，光強度の揺らぎの相関分布 G(x, y) は，

Ghost imaging eq02.png

となる．この G(x, y) が，サンプルのイメージとなる．すなわち，光強度の揺らぎの２次相関を計算していることになる．画像品質は，照明回数に依存して変化する．ゴーストイメージングは相関計算を用いていることから多数回の繰り返し照明が必要となる．そのため，少ない照明回数だと全体的にノイジーな画像となり画像品質は劣化する．なお，一般的には，光強度のみの計測であるが位相物体の計測の報告例[10]もある．

ゴーストイメージングの利点

図2 ゴーストイメージングの測定例と耐ノイズ性能

　ゴーストイメージングは，イメージの算出方法と光強度検出器に特徴がある．したがって，それらに起因した利点を有している．
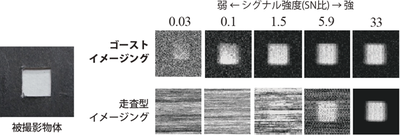
　強度の揺らぎの相関を計算していることから，ロックイン検出と同じアナロジーであり，すなわち，ゴーストイメージングは耐ノイズ性に優れたイメージング法とも言える．図２に，走査型イメージングにより取得した画像との比較を示す．検出光強度のSN比が低くなるにつれてゴーストイメージングが優位であることがわかる．この耐ノイズ性に優れたイメージング法であることは，当初，非常に弱い相互作用である光子の空間的なもつれの検出に利用されていたことからもうかがえる[1]．また，渋谷らの報告で定量的に評価され明らかにもされている[11]．
　点型検出器を用いることから，センシングできるデバイスが存在する物理量であればイメージングが可能と言える．例えば，電磁波はもとより，中性子線や電子線のような放射線さらには熱や音のイメージングも可能である．さらに，高速に変調された，2次元素子では検出不可能な信号によるイメージングもできる．また，結像光学系を必要としないため小型イメージングシステムの構築が可能であり，複数検出器による複数の特徴量（多波長，多角度など）を同時に計測することもできる．

投影する光強度分布 In(x, y) の考え方

　ゴーストイメージングで用いる光強度分布 In(x, y) は様々な考え方があり興味深い．例えば，ゴーストイメージングで得られる画像の品質は，投影する光強度分布 In(x, y) に依存する．例えば，画像の空間分解能は照明する光強度分布 In(x, y) の空間分解能とほぼ同じと考えて良い．ゴーストイメージングが提案された初期の頃は，光強度分布を得るためにスキャニングしていた[1]が，その後，スペックルパターンを用いることで空間分解能の高い分布を得ることが可能になった．さらに，プロジェクタを用いていることから計算機ゴーストイメージングの解像度はプロジェクタの投影解像度に依存する．なお，いずれの場合も，光源と被撮影物体間にあるレンズ等の投影光学系に影響される．
　また，確率的な事象の検出に端を発しているため，ランダムな光強度分布 In(x, y) を用いていた．しかし，空間周波数という捉え方をした効率的な照明方法，例えば，アダマール行列を基にした照明方法も提案されている[11]．

応用

　上記特徴を利用した応用が報告されている．例えば，非常に擾乱の多い媒質中でのイメージング[12]，テラヘルツイメージング[13], 建物の距離計測[14], 分光イメージング[15]，三次元形状計測[16]などがある．

学術的位置付け

　近年，点型検出器を用いたイメージング方法をシングルピクセルイメージングと呼んでいる．さらに，シングルピクセルイメージングは，イメージの再構成方法で分類され，相関計算により求めるゴーストイメージングと解析的に求めるコンプレッシブセンシングに分けられる．一般的に，感度を求めるならゴーストイメージング，高速性を求めるならコンプレッシブセンシングと使い分けている．

外部リンク

引用

  1. ↑ 1.0 1.1 1.2 T. B. Pittman, Y. H. Shih, D. V. Strekalov, and A. V. Sergienko, "Optical imaging by means of two-photon quantum entanglement," Phys. Rev. A, 52, R3429 (1995).
  2. ↑ A. V. Belinsky and D. N. Klyshko, "Two-photon optics diffraction holography and transformation of two-dimensional signals," Sov. Phys. JETP, 78, 259 (1994).
  3. ↑ D. V. Strekalov, A. V. Sergienko, D. N. Klyshko, and Y. H. Shih, “Observation of Two-Photon “Ghost” Interference and Diffraction,” Phys. Rev. Lett, 74, 3600 (1995).
  4. ↑ R. S. Bennink, S. J. Bentley, and R. W. Boyd, "“Two-photon” coincidence imaging with a classical source," Phys. Rev. Lett., 89, 113601 (2002).
  5. ↑ A. Gatti, E. Brambilla, M. Bache, and L. A. Lugiato, "Ghost imaging with thermal light: comparing entanglement and classical correlation," Phys. Rev. Lett., 93, 093602 (2004).
  6. ↑ F. Ferri, D. Magatti, A. Gatti, M. Bache, E. Brambilla, and L. A. Lugiato, "High-Resolution ghost image and ghost diffraction experiments with thermal light," Phys. Rev. Lett., 94, 183602 (2005).
  7. ↑ B. I. Erkmen and J. H. Shapiro, "Unified theory of ghost imaging with Gaussian-state light," Phys. Rev. A, 77, 043809 (2008).
  8. ↑ Y. Bromberg, O. Katz, and Y. Silberberg, "Ghost imaging with a single detector," Phys. Rev. A, 79, 053840 (2009).
  9. ↑ J. H. Shapiro, "Computational ghost imaging," Phys. Rev. A, 78, 061802(R) (2008).
  10. ↑ T. Shirai, T. Setala, and A. T. Friberg, "Ghost imaging of phase objects with classical incoherent light," Phys. Rev. A, 84, 041801(R) (2011).
  11. ↑ 11.0 11.1 K. Shibuya, K. Nakae, Y. Mizutani, T, Iwata, “Comparison of reconstructed images between ghost imaging and Hadamard transform imaging,” Optical Review，22, 897 (2015).
  12. ↑ R. E. Meyers, K. S. Deacon, Y. Shih, “Turbulence-free ghost imaging,” Appl. Phys. Lett., 98 111115 (2011).
  13. ↑ Z. Xu, E.Y. Lam, "Image reconstruction using spectroscopic and hyperspectral information for compressive terahertz imaging," J. Opt. Soc. Am. A, 27, 1638 (2010).
  14. ↑ X. Xu, E. Li, H. Yu, W. Gong, S. Han, “Morphology separation in ghost imaging via sparsity constraint,” Optics Express, 22, 14375 (2014).
  15. ↑ SS. Welsh, et al. SPIE MOEMS-MEMS. International Society for Optics and Photonics, (2013).
  16. ↑ B. Sun, M. P. Edgar, R. Bowman, L.E. Vittert, S. Welsh, A. Bowman, M.J. Padgett, “3D Computational Imaging with Single-Pixel Detectors,” Science. 340, 844, (2013).


「http://precipedia.jspe.or.jp/wiki/index.php?title=ゴーストイメージング&oldid=1573」から取得