「点群面張り」の版間の差分

提供: Precipedia
移動: 案内、 検索
7行: 7行:
 
===手法===
 
===手法===
  
−
初期の手法としてはBoissonnatによる陽的手法<ref name="ref1">J.-D. Boissonnat, Geometric structures for three-dimensional shape representation. ACM Trans. Graph. 3, 4 (1984) 266.</ref>が知られている。またHoppeらによる手法<ref name="ref2">H. Hoppe, T. Derose, T. Duchamp, J. Mcdonald, W. Stuetzle: Surface reconstruction from unorganized points. SIGGRAPH Comput. Graph. 26, 2 (1992) 71.</ref>は陰的手法の先駆けである。
+
初期の手法としてはBoissonnatによる陽的手法<ref name="ref1">J.-D. Boissonnat, Geometric structures for three-dimensional shape representation. ACM Trans. Graph. 3, 4 (1984) 266.</ref>が知られている。またHoppeらによる手法<ref name="ref2">H. Hoppe, T. Derose, T. Duchamp, J. Mcdonald, W. Stuetzle: Surface reconstruction from unorganized points. SIGGRAPH Comput. Graph. 26, 2 (1992) 71.</ref>は陰的手法の先駆けである。
  
−
表面再構成法は、入力点をメッシュ頂点として用いる陽的手法<ref name="ref1"></ref><ref>N. Amenta, M. Bern, M. Kamvysselis: A new Voronoi-based surface reconstruction algorithm. In Proceedings of the 25th annual conference on Computer graphics and interactive techniques, (1998) 415.</ref><ref>T. K. Dey, and J. Giesen. Detecting undersampling in surface reconstruction.  In Proceedings of the 17th ACM Symposium on Computational Geometry (2001),  257--263.</ref> と、入力点を基に何らかの関数場を生成してその等値面をメッシュ化する陰的手法<ref name="ref2"></ref><ref>Y. Ohtake, A. Belyaev, M. Alexa, G. Turk, H.-P. Seidel. Multi-level partition of unity implicits. ACM Trans. Graph. 22, 3 (2003), 463.</ref><ref>M. Kazhdan, M. Bolitho, H. Hoppe. Poisson surface reconstruction. In Proceedings of Symposium on Geometry Processing 2006, 61-70.</ref>に大別される（図２）。
+
表面再構成法は、入力点をメッシュ頂点として用いる陽的手法<ref name="ref1"></ref><ref>N. Amenta, M. Bern, M. Kamvysselis: A new Voronoi-based surface reconstruction algorithm. In Proceedings of the 25th annual conference on Computer graphics and interactive techniques, (1998) 415.</ref><ref>T. K. Dey, and J. Giesen. Detecting undersampling in surface reconstruction.  In Proceedings of the 17th ACM Symposium on Computational Geometry (2001),  257--263.</ref> と、入力点を基に何らかの関数場を生成してその等値面をメッシュ化する陰的手法<ref name="ref2"></ref><ref>Y. Ohtake, A. Belyaev, M. Alexa, G. Turk, H.-P. Seidel. Multi-level partition of unity implicits. ACM Trans. Graph. 22, 3 (2003), 463.</ref><ref>M. Kazhdan, M. Bolitho, H. Hoppe. Poisson surface reconstruction. In Proceedings of Symposium on Geometry Processing 2006, 61-70.</ref>に大別される（図２）。
  
−
陽的手法の中には、サンプリングされたオブジェクトの表面に対する出力メッシュの誤差の上限が保証されているものもあり、精度を重視する応用先で採用されている。ただし入力点群がそのまま出力メッシュの頂点になるため、点群中のノイズや密度差による影響を受けやすいといった問題がある。一方、陰的手法は近似手法であるためノイズや密度差による影響を受けにくいが、精度の保証は難しい。入力データ・応用先に適した手法を選ぶことが肝要である。手法のまとめは<ref>長井 超慧, 3D スキャナによる計算機への現物形状入力 Geometry Interface for 3D Scanning. 精密工 学会誌，精密工学会，Vol. 79, No. 6, pp.497-501, 2013.</ref><ref>M. Berger, A. Tagliasacchi, L. M. Seversky, P. Alliez, G. Guennebaud, J. A. Levine,
+
陽的手法の中には、サンプリングされたオブジェクトの表面に対する出力メッシュの誤差の上限が保証されているものもあり、精度を重視する応用先で採用されている。ただし入力点群がそのまま出力メッシュの頂点になるため、点群中のノイズや密度差による影響を受けやすいといった問題がある。一方、陰的手法は近似手法であるためノイズや密度差による影響を受けにくいが、精度の保証は難しい。入力データ・応用先に適した手法を選ぶことが肝要である。手法のまとめは<ref>長井 超慧, 3D スキャナによる計算機への現物形状入力 Geometry Interface for 3D Scanning. 精密工 学会誌，精密工学会，Vol. 79, No. 6, pp.497-501, 2013.</ref><ref>M. Berger, A. Tagliasacchi, L. M. Seversky, P. Alliez, G. Guennebaud, J. A. Levine,
 
A. Sharf, C. T. Silva, A Survey of Surface Reconstruction from Point Clouds. Computer Graphics Forum, 2016. DOI: 10.1111/cgf.12802</ref>などを参照されたい。
 
A. Sharf, C. T. Silva, A Survey of Surface Reconstruction from Point Clouds. Computer Graphics Forum, 2016. DOI: 10.1111/cgf.12802</ref>などを参照されたい。
  
−
通常、実用に足るメッシュを得るには、点群に含まれるノイズ・欠損・異常値・密度差等を軽減する前処理や、メッシュのスムージングや穴埋めといった後処理が必要である。
+
通常、実用に足るメッシュを得るには、点群に含まれるノイズ・欠損・異常値・密度差等を軽減する前処理や、メッシュのスムージングや穴埋めといった後処理が必要である。
 
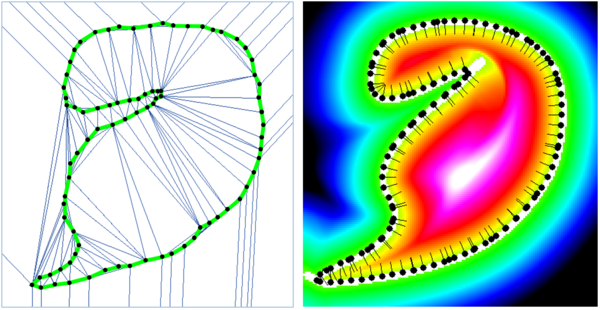
[[画像:SR-methods.PNG|thumb|600px|center|2次元の点群（黒点）に対する陽的手法（左）と陰的手法（右）の概念図。左図のうち、緑の線が陽的手法で得られるメッシュを、青の線が中間データを示している。右図の色は陰的手法で生成された関数の値を表しており、白色の線がオブジェクト表面を表現する等高線となっている。黒色の線は各店における法線ベクトルである。]]
 
[[画像:SR-methods.PNG|thumb|600px|center|2次元の点群（黒点）に対する陽的手法（左）と陰的手法（右）の概念図。左図のうち、緑の線が陽的手法で得られるメッシュを、青の線が中間データを示している。右図の色は陰的手法で生成された関数の値を表しており、白色の線がオブジェクト表面を表現する等高線となっている。黒色の線は各店における法線ベクトルである。]]
  

2017年2月21日 (火) 13:57時点における版

点群面張り（surface reconstruction）とは、あるオブジェクトの表面からサンプリングされたと考えられる点集合（点群）が与えられたとき、サンプル元のオブジェクト表面を表すメッシュを生成する問題を指す。表面再構成ともいう。またこの問題を解決する手法を表面再構成法という。

目次

詳細

点群面張りの最も一般的な例は、光学式3次元表面スキャナで取得した点群を表面メッシュに変換するというもので（図１）、リバースエンジニアリングや３Dプリンタへの入力データ生成を目的として行われることが多い。

ファイル:SR.png
点群面張りの概要。オブジェクト（写真）の光学式スキャンで得た点群（左）と表面メッシュ（右）。

手法

初期の手法としてはBoissonnatによる陽的手法[1]が知られている。またHoppeらによる手法[2]は陰的手法の先駆けである。

表面再構成法は、入力点をメッシュ頂点として用いる陽的手法[1][3][4] と、入力点を基に何らかの関数場を生成してその等値面をメッシュ化する陰的手法[2][5][6]に大別される（図２）。

陽的手法の中には、サンプリングされたオブジェクトの表面に対する出力メッシュの誤差の上限が保証されているものもあり、精度を重視する応用先で採用されている。ただし入力点群がそのまま出力メッシュの頂点になるため、点群中のノイズや密度差による影響を受けやすいといった問題がある。一方、陰的手法は近似手法であるためノイズや密度差による影響を受けにくいが、精度の保証は難しい。入力データ・応用先に適した手法を選ぶことが肝要である。手法のまとめは[7][8]などを参照されたい。

通常、実用に足るメッシュを得るには、点群に含まれるノイズ・欠損・異常値・密度差等を軽減する前処理や、メッシュのスムージングや穴埋めといった後処理が必要である。

2次元の点群（黒点）に対する陽的手法（左）と陰的手法（右）の概念図。左図のうち、緑の線が陽的手法で得られるメッシュを、青の線が中間データを示している。右図の色は陰的手法で生成された関数の値を表しており、白色の線がオブジェクト表面を表現する等高線となっている。黒色の線は各店における法線ベクトルである。

関連項目

引用

  1. ↑ 1.0 1.1 J.-D. Boissonnat, Geometric structures for three-dimensional shape representation. ACM Trans. Graph. 3, 4 (1984) 266.
  2. ↑ 2.0 2.1 H. Hoppe, T. Derose, T. Duchamp, J. Mcdonald, W. Stuetzle: Surface reconstruction from unorganized points. SIGGRAPH Comput. Graph. 26, 2 (1992) 71.
  3. ↑ N. Amenta, M. Bern, M. Kamvysselis: A new Voronoi-based surface reconstruction algorithm. In Proceedings of the 25th annual conference on Computer graphics and interactive techniques, (1998) 415.
  4. ↑ T. K. Dey, and J. Giesen. Detecting undersampling in surface reconstruction. In Proceedings of the 17th ACM Symposium on Computational Geometry (2001), 257--263.
  5. ↑ Y. Ohtake, A. Belyaev, M. Alexa, G. Turk, H.-P. Seidel. Multi-level partition of unity implicits. ACM Trans. Graph. 22, 3 (2003), 463.
  6. ↑ M. Kazhdan, M. Bolitho, H. Hoppe. Poisson surface reconstruction. In Proceedings of Symposium on Geometry Processing 2006, 61-70.
  7. ↑ 長井 超慧, 3D スキャナによる計算機への現物形状入力 Geometry Interface for 3D Scanning. 精密工 学会誌，精密工学会，Vol. 79, No. 6, pp.497-501, 2013.
  8. ↑ M. Berger, A. Tagliasacchi, L. M. Seversky, P. Alliez, G. Guennebaud, J. A. Levine, A. Sharf, C. T. Silva, A Survey of Surface Reconstruction from Point Clouds. Computer Graphics Forum, 2016. DOI: 10.1111/cgf.12802
「http://precipedia.jspe.or.jp/wiki/index.php?title=点群面張り&oldid=1607」から取得