「美的曲線」の版間の差分

提供: Precipedia
移動: 案内、 検索
(ページの作成:「{{subst:Temp}}」)
 
1行: 1行:
−
これは用語説明を作成する際のテンプレートです。
+
<b>美的曲線</b>(log-aesthetic curve)は、αというパラメータによって、クロソイド曲線(α=-1)、Nielsenのらせん(α=0)、対数らせん(α=1)、円のインボリュート曲線(α=2)を一般化させた曲線である。美的曲線は、対数美的曲線、対数型美的曲線とも呼ばれる。
−
不必要な文章を適時修正・消去してご利用ください。
+
−
 
+
−
まずは文頭で用語の定義を簡潔に記述ください。
+
−
Wikipedia<ref>MediaWikiを利用している辞書作成プロジェクトです。</ref>では、
+
−
 
+
−
<b>○○</b>(英語表記)は、～～～～で、～～～～である。
+
−
 
+
−
と冒頭に定義を行い、その後追加で説明を行うスタイルを推奨しています。
+
−
 
+
  
 
==詳細==
 
==詳細==
 +
===装置===
 +
[[画像:XCT.png|thumb|200px|right|X線CT装置の概念図]]
 +
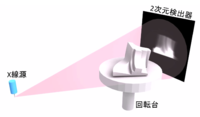
スキャンの方式としては、検出器が1次元のファンビーム型と、検出器が2次元のコーンビーム型が代表的である。図1にコーンビーム型方式の模式図を示す。ファンビーム型は1回転で1断面のみスキャン可能なのに対して、コーンビーム型は1回転すれば全ての断面にあたるボリュームを取得できるため測定スピードに関して大きなアドバンテージがある。一方で、検出器が1次元である場合にはX線の散乱線対策であるコリメータの構築が容易であり、特に散乱線の影響が大きい高エネルギX線源を用いる装置ではファンビーム型が採用されることが多い。
  
−
[[画像:usage_sample.png|thumb|right|掲載例]]
 
−
上の説明だけでは足りない場合や、細かな分類を挙げてそれぞれの特徴を論じる場合には適切なタイトルをつけて記述を追加ください。
 
−
見出しの追加により、複数の事項についての記述を行うことができます。
 
−
 
−
===図表の追加===
 
−
また、写真や図面を利用する場合は、適切なサイズを用いたサムネールを設定し、枠を画面の右側に配置することをお勧めします
 
−
<ref>本テンプレートにもありますが、セクションの冒頭にリンクを作成することで文章がうまく図表の左側に回りこみます</ref>。
 
−
 
−
==関連項目==
 
−
 
−
関連する用語がPrecipediaに掲載され、これらを合わせて閲覧することでさらに用語への理解が深まる場合には、ぜひそれらの用語へのリンクを作成ください。
 
−
また、該当する用語が存在しない場合には、ここにリンクを作成した後にクリックすることで作成を開始することができます。
 
−
 
−
*[[用語1]]
 
−
*[[用語2]]
 
−
*[[用語3]]
 
−
 
−
==外部リンク==
 
−
 
−
執筆者の所属研究組織、製品製造企業など、これらを合わせて閲覧することでさらに用語への理解が深まるサイトが存在する場合は
 
−
ぜひそれらへのリンクを作成ください。
 
  
−
*[http://www.hogehoge.ac.jp/mech/hogehoge ほげほげ大学工学部機械工学科ほげほげ研究室]<ref>架空のリンクです</ref>
+
===データ処理===
−
*[http://www.hogehoge.co.jp/hogehoge ほげほげ株式会社ほげほげ事業部]
+
[[画像:XCT-data.png|thumb|200px|right|X線CTのデータ処理]]
 +
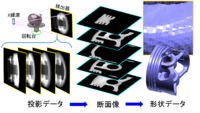
装置からの直接的な出力はX線の投影データ（サイノグラム）であり、計算機上でCT再構成)<ref>1. Jiang Hsieh, Computed Tomography: Principles, Design, Artifacts, and Recent Advances, SPIE Press, 2003</ref>を行うことにより断面像（トモグラム）を得る。寸法計測のために形状データが必要な場合には、断面像上で注目する物体とそれ以外の領域の境界面をポリゴンメッシュとして抽出する。図2にこれらの処理の例を示す。
  
 
==引用==
 
==引用==
45行: 19行:
  
 
----
 
----
−
記入の最後には、必ず用語の読み方とカテゴリに関する情報を追加するようにしてください。
 
  
−
  {{DEFAULTSORT:}}
+
  {{DEFAULTSORT:さんぎょうようえっくすせんしーてぃー}}
−
  [[Category:]]
+
  [[Category:総目次]]

2016年8月1日 (月) 19:11時点における版

美的曲線(log-aesthetic curve)は、αというパラメータによって、クロソイド曲線(α=-1)、Nielsenのらせん(α=0)、対数らせん(α=1)、円のインボリュート曲線(α=2)を一般化させた曲線である。美的曲線は、対数美的曲線、対数型美的曲線とも呼ばれる。

目次

詳細

装置

X線CT装置の概念図

スキャンの方式としては、検出器が1次元のファンビーム型と、検出器が2次元のコーンビーム型が代表的である。図1にコーンビーム型方式の模式図を示す。ファンビーム型は1回転で1断面のみスキャン可能なのに対して、コーンビーム型は1回転すれば全ての断面にあたるボリュームを取得できるため測定スピードに関して大きなアドバンテージがある。一方で、検出器が1次元である場合にはX線の散乱線対策であるコリメータの構築が容易であり、特に散乱線の影響が大きい高エネルギX線源を用いる装置ではファンビーム型が採用されることが多い。


データ処理

X線CTのデータ処理

装置からの直接的な出力はX線の投影データ（サイノグラム）であり、計算機上でCT再構成)[1]を行うことにより断面像（トモグラム）を得る。寸法計測のために形状データが必要な場合には、断面像上で注目する物体とそれ以外の領域の境界面をポリゴンメッシュとして抽出する。図2にこれらの処理の例を示す。

引用

原著論文、著書など、他に著作権の存在する出版物等を引用する場合は、ここに脚注のリストを表示するようにしてください。

  1. ↑ 1. Jiang Hsieh, Computed Tomography: Principles, Design, Artifacts, and Recent Advances, SPIE Press, 2003


「http://precipedia.jspe.or.jp/wiki/index.php?title=美的曲線&oldid=1463」から取得