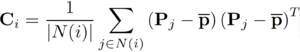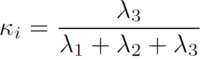「点群特徴抽出」の版間の差分
JSPEreviewer (トーク | 投稿記録) |
JSPEreviewer (トーク | 投稿記録) |
||
| (1人の利用者による、間の2版が非表示) | |||
| 9行: | 9行: | ||
点群の主成分分析(Principal Component Analysis,PCA)は,点群中の各点における法線や曲率の推定,周辺点群の分布状態推定,姿勢に依存しない局所座標系定義に用いられる.点群の点 ''i'' の近傍点集合 ''N(i)'' に対する主成分分析は,次の分散共分散行列(Variance-covariance matrix)'''C'''<sub>''i''</sub> の固有値解析により行われる. | 点群の主成分分析(Principal Component Analysis,PCA)は,点群中の各点における法線や曲率の推定,周辺点群の分布状態推定,姿勢に依存しない局所座標系定義に用いられる.点群の点 ''i'' の近傍点集合 ''N(i)'' に対する主成分分析は,次の分散共分散行列(Variance-covariance matrix)'''C'''<sub>''i''</sub> の固有値解析により行われる. | ||
| − | [[ファイル:tenguntokutyo-eq1.PNG | + | [[ファイル:tenguntokutyo-eq1.PNG|center|300px]] |
ここで,'''p'''<sub>''j''</sub> は点 ''j'' の位置(列ベクトル),<span style="text-decoration:overline;">'''p'''</span> は ''N(i)'' の重心,|''N(i)''| は ''N(i)'' の点数である.近傍点集合 ''N(i)'' は,点 ''i'' に近いほうから ''k'' 個の点集合(''k''近傍)や,点 ''i'' を中心とする半径 ''r'' の球内の点集合が用いられる.行列 '''C'''<sub>''i''</sub> の得られた固有値を λ<sub>1</sub>, λ<sub>2</sub>, λ<sub>3</sub> ( λ<sub>1</sub>≥λ<sub>2</sub>≥λ<sub>3</sub> ),対応する固有ベクトルを '''e'''<sub>1</sub>, '''e'''<sub>2</sub>, '''e'''<sub>3</sub> とすると,'''e'''<sub>1</sub> は ''N(i)'' の分散(ばらつき)が最大の方向となり,'''e'''<sub>2</sub> は,'''e'''<sub>1</sub> に直交するなかで分散が最大となる方向,'''e'''<sub>3</sub> は分散が最小の方向となる.各固有値は,対応する固有ベクトルの方向に沿った ''N(i)'' の分散となる.主成分分析の結果より,点群の点 ''i'' における法線ベクトル '''n'''<sub>''i''</sub> と近似曲率 κ<sub>''i''</sub>(図1),次元特徴 ''d<sub>i</sub>'' は以下の通り求められる. | ここで,'''p'''<sub>''j''</sub> は点 ''j'' の位置(列ベクトル),<span style="text-decoration:overline;">'''p'''</span> は ''N(i)'' の重心,|''N(i)''| は ''N(i)'' の点数である.近傍点集合 ''N(i)'' は,点 ''i'' に近いほうから ''k'' 個の点集合(''k''近傍)や,点 ''i'' を中心とする半径 ''r'' の球内の点集合が用いられる.行列 '''C'''<sub>''i''</sub> の得られた固有値を λ<sub>1</sub>, λ<sub>2</sub>, λ<sub>3</sub> ( λ<sub>1</sub>≥λ<sub>2</sub>≥λ<sub>3</sub> ),対応する固有ベクトルを '''e'''<sub>1</sub>, '''e'''<sub>2</sub>, '''e'''<sub>3</sub> とすると,'''e'''<sub>1</sub> は ''N(i)'' の分散(ばらつき)が最大の方向となり,'''e'''<sub>2</sub> は,'''e'''<sub>1</sub> に直交するなかで分散が最大となる方向,'''e'''<sub>3</sub> は分散が最小の方向となる.各固有値は,対応する固有ベクトルの方向に沿った ''N(i)'' の分散となる.主成分分析の結果より,点群の点 ''i'' における法線ベクトル '''n'''<sub>''i''</sub> と近似曲率 κ<sub>''i''</sub>(図1),次元特徴 ''d<sub>i</sub>'' は以下の通り求められる. | ||
| 24行: | 24行: | ||
<gallery widths="300px" heights="300px"> | <gallery widths="300px" heights="300px"> | ||
| − | ファイル:tenguntokutyo-Fig1.PNG | + | ファイル:tenguntokutyo-Fig1.PNG|図1 近似曲率<ref name="ref1"></ref> |
ファイル:tenguntokutyo-Fig2.PNG|図2 次元特徴量 | ファイル:tenguntokutyo-Fig2.PNG|図2 次元特徴量 | ||
</gallery> | </gallery> | ||
| 30行: | 30行: | ||
==マルチスケールに基づく特徴抽出== | ==マルチスケールに基づく特徴抽出== | ||
| − | |||
| − | |||
マルチスケールに基づく特徴抽出法では,複数のスケール(近傍半径や近傍点数)で定義される複数の近傍点集合から特徴量を抽出し,得られた複数の特徴量を用いて最終的な特徴量を算出する.対象物のスケールの差異やノイズに対する頑健性の改善や,単独スケールに比べてより高度で安定した特徴量の抽出を可能としており,エッジやコーナー,段差等の特徴形状部の検出等に利用されている. | マルチスケールに基づく特徴抽出法では,複数のスケール(近傍半径や近傍点数)で定義される複数の近傍点集合から特徴量を抽出し,得られた複数の特徴量を用いて最終的な特徴量を算出する.対象物のスケールの差異やノイズに対する頑健性の改善や,単独スケールに比べてより高度で安定した特徴量の抽出を可能としており,エッジやコーナー,段差等の特徴形状部の検出等に利用されている. | ||
:* 頑固な(Persistent)特徴 <ref name="ref3"></ref> | :* 頑固な(Persistent)特徴 <ref name="ref3"></ref> | ||
| − | 複数のスケールで定義された近傍点集合のそれぞれに対して主成分分析を用いて近似曲率を求め,閾値よりも大きな近似曲率値の個数を特徴量とする.スケールの異なる近傍点集合に対して安定して大きな近似曲率値が得られる点は特徴量の値が高くなり,エッジやコーナー部で高い値となる. | + | :: 複数のスケールで定義された近傍点集合のそれぞれに対して主成分分析を用いて近似曲率を求め,閾値よりも大きな近似曲率値の個数を特徴量とする.スケールの異なる近傍点集合に対して安定して大きな近似曲率値が得られる点は特徴量の値が高くなり,エッジやコーナー部で高い値となる. |
:* Difference of Normal (DoN,図3) <ref name="ref4"></ref> | :* Difference of Normal (DoN,図3) <ref name="ref4"></ref> | ||
| − | 異なる2つの近傍半径 ''r<sub>l</sub>'', ''r<sub>s</sub>'' (''r<sub>l</sub>'' > ''r<sub>s</sub>'') を用いて点 ''i'' の近傍点集合を求め,それぞれに対して法線ベクトル '''n'''(''i'', ''r<sub>l</sub>''), '''n'''(''i'', ''r<sub>s</sub>'') を求める.そして,求めた2つの法線ベクトルの差分で定義されるベクトル Δ'''n''' (次式)がDoNの特徴量となる. | + | :: 異なる2つの近傍半径 ''r<sub>l</sub>'', ''r<sub>s</sub>'' (''r<sub>l</sub>'' > ''r<sub>s</sub>'') を用いて点 ''i'' の近傍点集合を求め,それぞれに対して法線ベクトル '''n'''(''i'', ''r<sub>l</sub>''), '''n'''(''i'', ''r<sub>s</sub>'') を求める.そして,求めた2つの法線ベクトルの差分で定義されるベクトル Δ'''n''' (次式)がDoNの特徴量となる. |
| − | [[ファイル:tenguntokutyo-eq5.PNG|center| | + | [[ファイル:tenguntokutyo-eq5.PNG|center|300px]] |
特徴量のノルムは,エッジやコーナー上では値が低く,その周辺で高い値となり,荒れた面や段差の検出に向いている. | 特徴量のノルムは,エッジやコーナー上では値が低く,その周辺で高い値となり,荒れた面や段差の検出に向いている. | ||
:* Difference of Center of Gravity(DoCoG)<ref name="ref5"></ref> | :* Difference of Center of Gravity(DoCoG)<ref name="ref5"></ref> | ||
| − | DoCoGでは,異なる2つの近傍半径を用いて点 ''i'' の近傍点集合を求め,それぞれの重心点間距離を点 ''i'' の特徴量とする.コーナー,エッジ,平坦な領域の順に特徴量の値が小さくなり,それらの区別が可能である一方で,遮蔽による点群境界部付近において値が高くなる.この問題を解決するための,点群と重心点との距離評価を用いた拡張法(Classified DoCoG)も提案されている. | + | :: DoCoGでは,異なる2つの近傍半径を用いて点 ''i'' の近傍点集合を求め,それぞれの重心点間距離を点 ''i'' の特徴量とする.コーナー,エッジ,平坦な領域の順に特徴量の値が小さくなり,それらの区別が可能である一方で,遮蔽による点群境界部付近において値が高くなる.この問題を解決するための,点群と重心点との距離評価を用いた拡張法(Classified DoCoG)も提案されている. |
| + | |||
| + | <gallery widths="300px" heights="200px"> | ||
| + | ファイル:tenguntokutyo-Fig3.PNG|図3 DoN | ||
| + | </gallery> | ||
==高次元の特徴記述法== | ==高次元の特徴記述法== | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
レジストレーションや物体認識のための形状間の対応抽出や多種曲面の識別では,各点において,曲率や法線等の基礎緒量のみならず,より多くの形状の特徴を定量評価できる特徴量が有効となる.このために,近傍点集合の画像化,近傍点集合内の点の組み合わせ評価,近傍点集合の分割と各分割点集合の分析等を用いたさまざまな特徴記述法が提案されている.この方法は,特に,モデルベースの物体認識(事前に用意した3Dモデルと計測データとのマッチングによる物体認識)において用いられている. | レジストレーションや物体認識のための形状間の対応抽出や多種曲面の識別では,各点において,曲率や法線等の基礎緒量のみならず,より多くの形状の特徴を定量評価できる特徴量が有効となる.このために,近傍点集合の画像化,近傍点集合内の点の組み合わせ評価,近傍点集合の分割と各分割点集合の分析等を用いたさまざまな特徴記述法が提案されている.この方法は,特に,モデルベースの物体認識(事前に用意した3Dモデルと計測データとのマッチングによる物体認識)において用いられている. | ||
:* Spin Image(図4)<ref name="ref6"></ref> | :* Spin Image(図4)<ref name="ref6"></ref> | ||
| − | Spin imageは,画像を用いて近傍点集合を表す特徴記述法である.ある点 ''i'' のSpin imageは,点 ''i'' の位置とその法線ベクトルで定義される直線からの距離,ならびに,点 ''i'' の接平面からの距離で定義される2次元平面に近傍点集合の各点を投影し,投影面上に定義したグリッドへの双一次補間に基づく投票処理により生成される. | + | :: Spin imageは,画像を用いて近傍点集合を表す特徴記述法である.ある点 ''i'' のSpin imageは,点 ''i'' の位置とその法線ベクトルで定義される直線からの距離,ならびに,点 ''i'' の接平面からの距離で定義される2次元平面に近傍点集合の各点を投影し,投影面上に定義したグリッドへの双一次補間に基づく投票処理により生成される. |
:* PFH(Point Feature Histogram,図5)<ref name="ref1"></ref> | :* PFH(Point Feature Histogram,図5)<ref name="ref1"></ref> | ||
| − | PFHは,近傍点集合内の点対評価を用いたヒストグラムベースの特徴記述法である.点 ''i'' の近傍点集合内の点対に対して,法線ベクトルと点位置の差分ベクトルから定められる3つの角度ならびに点間距離の4つの量を求める.各量を ''b'' 個の区分に分けた ''b''<sup>4</sup> 個のビンを生成し,各点対で求めた値を用いて作成したヒストグラムがPFHとなる.また,近傍点集合内の用いる点対の数を減らし,計算量を低減したものがFPFHである. | + | :: PFHは,近傍点集合内の点対評価を用いたヒストグラムベースの特徴記述法である.点 ''i'' の近傍点集合内の点対に対して,法線ベクトルと点位置の差分ベクトルから定められる3つの角度ならびに点間距離の4つの量を求める.各量を ''b'' 個の区分に分けた ''b''<sup>4</sup> 個のビンを生成し,各点対で求めた値を用いて作成したヒストグラムがPFHとなる.また,近傍点集合内の用いる点対の数を減らし,計算量を低減したものがFPFHである. |
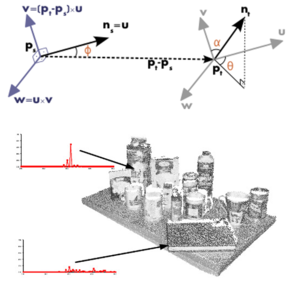
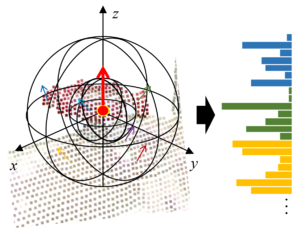
:* SHOT(Signature of Histograms of OrienTations,図6)<ref name="ref7"></ref> | :* SHOT(Signature of Histograms of OrienTations,図6)<ref name="ref7"></ref> | ||
| − | SHOTは,近傍点集合を分割した部分近傍点集合内の法線分布のヒストグラムをならべた特徴記述法である.点 ''i'' を中心とする球を定義し,その球を,半径方向に2分割,局所座標系のz軸(法線)方向に2分割,z軸周りに8分割した計32個の領域を生成する.そして,各領域に含まれる近傍点集合の点と点 ''i'' の法線ベクトル間の内積のヒストグラムを求め,それらを並べたベクトル(32 × ヒストグラムのビン数の次元)が点 ''i'' のSHOT特徴量となる.点が色情報を持つ場合には,色に対しても同様の特徴量を計算できる. | + | :: SHOTは,近傍点集合を分割した部分近傍点集合内の法線分布のヒストグラムをならべた特徴記述法である.点 ''i'' を中心とする球を定義し,その球を,半径方向に2分割,局所座標系のz軸(法線)方向に2分割,z軸周りに8分割した計32個の領域を生成する.そして,各領域に含まれる近傍点集合の点と点 ''i'' の法線ベクトル間の内積のヒストグラムを求め,それらを並べたベクトル(32 × ヒストグラムのビン数の次元)が点 ''i'' のSHOT特徴量となる.点が色情報を持つ場合には,色に対しても同様の特徴量を計算できる. |
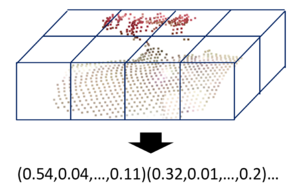
:* POD(Position and Orientation Distribution,図7)<ref name="ref8"></ref> | :* POD(Position and Orientation Distribution,図7)<ref name="ref8"></ref> | ||
| − | PODは,近傍点集合を分割した部分点集合の点の数や点分布に関する緒量をならべた特徴記述法である.主成分分析で求めた局所座標系を用いて点 ''i'' の近傍点集合を囲うBounding Boxを定義し,分散が最大の方向を4分割,分散が2番目に大きい方向を2分割した8つのセルを生成する.各セル内の近傍点の数,重心位置,分散共分散行列の対角と上三角成分をならべたベクトル(10次元)を求め,それらを並べたベクトル(80次元)がPOD特徴となる. | + | :: PODは,近傍点集合を分割した部分点集合の点の数や点分布に関する緒量をならべた特徴記述法である.主成分分析で求めた局所座標系を用いて点 ''i'' の近傍点集合を囲うBounding Boxを定義し,分散が最大の方向を4分割,分散が2番目に大きい方向を2分割した8つのセルを生成する.各セル内の近傍点の数,重心位置,分散共分散行列の対角と上三角成分をならべたベクトル(10次元)を求め,それらを並べたベクトル(80次元)がPOD特徴となる. |
幾つかの点群特徴抽出法は,フリーのオープンソースライブラリ <ref name="ref10">Point Cloud Library,http://pointclouds.org/</ref> で利用可能である. | 幾つかの点群特徴抽出法は,フリーのオープンソースライブラリ <ref name="ref10">Point Cloud Library,http://pointclouds.org/</ref> で利用可能である. | ||
| + | |||
| + | <gallery widths="300px" heights="300px"> | ||
| + | ファイル:tenguntokutyo-Fig4.PNG|図4 Spin Image | ||
| + | ファイル:tenguntokutyo-Fig5.PNG|図5 PFH <ref name="ref1"></ref> | ||
| + | ファイル:tenguntokutyo-Fig6.PNG|図6 SHOT | ||
| + | ファイル:tenguntokutyo-Fig7.PNG|図7 POD | ||
| + | </gallery> | ||
2018年2月22日 (木) 14:32時点における最新版
点群特徴抽出(Point cloud feature extraction)は,点群が表す形状の曲率や法線等の緒量を推定したり,形状の種々の特徴を定量的に表現する技術であり,レジストレーション,セグメンテーション,モデリングや物体認識等の点群処理の基礎となる.
目次[非表示] |
詳細
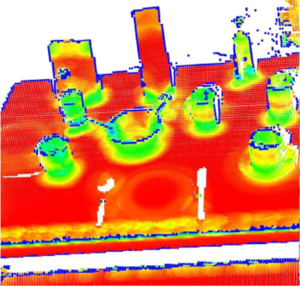
レーザ計測や画像計測で得られる物体や環境の3次元計測点群(point cloud)の幾何情報は,計測点の3次元座標値のみの集合であるため,そのままでは点群の用途が極めて限定される.点群の元となった曲面の法線や曲率等の形状に関する緒量を抽出したり,曲面の様々な特徴を定量的に表現する点群特徴抽出を行うことにより,点群の表す形状の理解,点群間の対応付け,点群内の類似した特徴を持つ部分の認識等が可能となり,レジストレーション(位置合わせ),セグメンテーション(領域分割),モデリング,物体認識など,さまざまな点群処理が可能となる.点群特徴抽出法には,点の密度や分布の違い,計測ノイズ,データの欠損に対して安定して効率よく特徴を抽出できることが望まれる.メッシュや陰関数,パラメトリック曲面等を介さずに,点群から直接的に特徴を抽出する方法として,法線や曲率等の基礎緒量を推定する主成分分析 [1][2],コーナーやエッジなどの特徴形状部の推定に有用なマルチスケール特徴抽出法 [3][4][5],形状の種々の特徴を定量的に表現できる高次元の特徴記述法 [1][6][7][8] 等が用いられている.より有用な特徴抽出法や特徴表現法の研究は,今もなお行われている.
主成分分析による基礎緒量の推定
点群の主成分分析(Principal Component Analysis,PCA)は,点群中の各点における法線や曲率の推定,周辺点群の分布状態推定,姿勢に依存しない局所座標系定義に用いられる.点群の点 i の近傍点集合 N(i) に対する主成分分析は,次の分散共分散行列(Variance-covariance matrix)Ci の固有値解析により行われる.
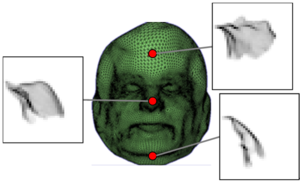
ここで,pj は点 j の位置(列ベクトル),p は N(i) の重心,|N(i)| は N(i) の点数である.近傍点集合 N(i) は,点 i に近いほうから k 個の点集合(k近傍)や,点 i を中心とする半径 r の球内の点集合が用いられる.行列 Ci の得られた固有値を λ1, λ2, λ3 ( λ1≥λ2≥λ3 ),対応する固有ベクトルを e1, e2, e3 とすると,e1 は N(i) の分散(ばらつき)が最大の方向となり,e2 は,e1 に直交するなかで分散が最大となる方向,e3 は分散が最小の方向となる.各固有値は,対応する固有ベクトルの方向に沿った N(i) の分散となる.主成分分析の結果より,点群の点 i における法線ベクトル ni と近似曲率 κi(図1),次元特徴 di は以下の通り求められる.
ここで,σ1 = λ1 ― λ2, σ2 = λ2 ― λ3, σ3 = λ3
次元特徴は,N(i) の分布の次元を表す(図2).また,主成分分析で得られる固有ベクトルの組は直交し,点群の位置姿勢に依存しないため,SHOTやPODなどの局所特徴記述のための局所座標系としても用いられている[7][8].
主成分分析で得られる緒量は,近傍点集合の選び方やノイズの影響を受けやすい.より頑健かつ正確な各緒量の推定のために,近傍点集合からの頑健なアウトライア除去 [9],重み付きの主成分分析 [1][7],エントロピー評価やマルチスケールに基づく最適近傍半径の自動決定 [2][3] といった方法が提案されている.また,主成分分析で得られる法線ベクトルの向きは,形状に対して外向きもしくは内向きに全てが揃っているとは限らない.この問題を解決するために,得られた法線を計測器の方向に向ける,もしくは近傍点と同様の向きに補正するなどの方法が用いられる [1].
図1 近似曲率[1]
マルチスケールに基づく特徴抽出
マルチスケールに基づく特徴抽出法では,複数のスケール(近傍半径や近傍点数)で定義される複数の近傍点集合から特徴量を抽出し,得られた複数の特徴量を用いて最終的な特徴量を算出する.対象物のスケールの差異やノイズに対する頑健性の改善や,単独スケールに比べてより高度で安定した特徴量の抽出を可能としており,エッジやコーナー,段差等の特徴形状部の検出等に利用されている.
- 頑固な(Persistent)特徴 [3]
- 複数のスケールで定義された近傍点集合のそれぞれに対して主成分分析を用いて近似曲率を求め,閾値よりも大きな近似曲率値の個数を特徴量とする.スケールの異なる近傍点集合に対して安定して大きな近似曲率値が得られる点は特徴量の値が高くなり,エッジやコーナー部で高い値となる.
- Difference of Normal (DoN,図3) [4]
- 異なる2つの近傍半径 rl, rs (rl > rs) を用いて点 i の近傍点集合を求め,それぞれに対して法線ベクトル n(i, rl), n(i, rs) を求める.そして,求めた2つの法線ベクトルの差分で定義されるベクトル Δn (次式)がDoNの特徴量となる.
特徴量のノルムは,エッジやコーナー上では値が低く,その周辺で高い値となり,荒れた面や段差の検出に向いている.
- Difference of Center of Gravity(DoCoG)[5]
- DoCoGでは,異なる2つの近傍半径を用いて点 i の近傍点集合を求め,それぞれの重心点間距離を点 i の特徴量とする.コーナー,エッジ,平坦な領域の順に特徴量の値が小さくなり,それらの区別が可能である一方で,遮蔽による点群境界部付近において値が高くなる.この問題を解決するための,点群と重心点との距離評価を用いた拡張法(Classified DoCoG)も提案されている.
高次元の特徴記述法
レジストレーションや物体認識のための形状間の対応抽出や多種曲面の識別では,各点において,曲率や法線等の基礎緒量のみならず,より多くの形状の特徴を定量評価できる特徴量が有効となる.このために,近傍点集合の画像化,近傍点集合内の点の組み合わせ評価,近傍点集合の分割と各分割点集合の分析等を用いたさまざまな特徴記述法が提案されている.この方法は,特に,モデルベースの物体認識(事前に用意した3Dモデルと計測データとのマッチングによる物体認識)において用いられている.
- Spin Image(図4)[6]
- Spin imageは,画像を用いて近傍点集合を表す特徴記述法である.ある点 i のSpin imageは,点 i の位置とその法線ベクトルで定義される直線からの距離,ならびに,点 i の接平面からの距離で定義される2次元平面に近傍点集合の各点を投影し,投影面上に定義したグリッドへの双一次補間に基づく投票処理により生成される.
- PFH(Point Feature Histogram,図5)[1]
- PFHは,近傍点集合内の点対評価を用いたヒストグラムベースの特徴記述法である.点 i の近傍点集合内の点対に対して,法線ベクトルと点位置の差分ベクトルから定められる3つの角度ならびに点間距離の4つの量を求める.各量を b 個の区分に分けた b4 個のビンを生成し,各点対で求めた値を用いて作成したヒストグラムがPFHとなる.また,近傍点集合内の用いる点対の数を減らし,計算量を低減したものがFPFHである.
- SHOT(Signature of Histograms of OrienTations,図6)[7]
- SHOTは,近傍点集合を分割した部分近傍点集合内の法線分布のヒストグラムをならべた特徴記述法である.点 i を中心とする球を定義し,その球を,半径方向に2分割,局所座標系のz軸(法線)方向に2分割,z軸周りに8分割した計32個の領域を生成する.そして,各領域に含まれる近傍点集合の点と点 i の法線ベクトル間の内積のヒストグラムを求め,それらを並べたベクトル(32 × ヒストグラムのビン数の次元)が点 i のSHOT特徴量となる.点が色情報を持つ場合には,色に対しても同様の特徴量を計算できる.
- POD(Position and Orientation Distribution,図7)[8]
- PODは,近傍点集合を分割した部分点集合の点の数や点分布に関する緒量をならべた特徴記述法である.主成分分析で求めた局所座標系を用いて点 i の近傍点集合を囲うBounding Boxを定義し,分散が最大の方向を4分割,分散が2番目に大きい方向を2分割した8つのセルを生成する.各セル内の近傍点の数,重心位置,分散共分散行列の対角と上三角成分をならべたベクトル(10次元)を求め,それらを並べたベクトル(80次元)がPOD特徴となる.
幾つかの点群特徴抽出法は,フリーのオープンソースライブラリ [10] で利用可能である.
図5 PFH [1]
関連項目
外部リンク
引用
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 Radu Bogdan Rusu, Semantic 3D Object Maps for Everyday Robot Manipulation, Springer (2013)
- ↑ 2.0 2.1 2.2 Jerome Demantké, Clément Mallet, Nicolas David, Bruno Vallet, Dimensionality based Scale Selection in 3D Lidar Point Clouds, ISPRS International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XXXVIII-5/WG12, 97-102 (2011)
- ↑ 3.0 3.1 3.2 Mark Pauly, Richard Keiser and Markus Gross, Multi-scale Feature Extraction on Point-Sampled Surfaces, Computer Graphics Forum, 22(3), 281-289 (2003)
- ↑ 4.0 4.1 Yani Ioannou, Babak Taati, Robin Harrap, Difference of Normals as a multi-scale Operator in Unorganized Point Clouds, Proc. The 2012 Second Int. Conf. on 3D Imaging, Modeling, Processing, Visualization & Transmission, 501-508 (2012)
- ↑ 5.0 5.1 早田赳,岩切宗利,重心移動を用いた3次元点群からの特徴抽出法,情報処理学会インタラクション2016, 1085-1087 (2016)
- ↑ 6.0 6.1 Andrew Johnson, Spin-Images: A Representation for 3-D Surface Matching, doctoral dissertation, The Robotics Institute, Carnegie Mellon University, (1997)
- ↑ 7.0 7.1 7.2 7.3 Samuele Salti, Federico Tombari, and Luigi Di Stefano, SHOT: Unique Signatures of Histograms for Surface and Texture Description, Computer Vision and Image Understanding, 125, 251-264 (2014)
- ↑ 8.0 8.1 8.2 Takahiko Furuya, and Ryutarou Ohbuchi, Diffusion-on-Manifold Aggregation of Local Features for Shape-based 3D Model Retrieval, Proc. ACM International Conference on Multimedia Information Retrieval, (2015)
- ↑ Abdul Nurunnabi, David Belton and Geoff West, Robust Segmentation in Laser Scanning 3D Point Cloud Data, Proc. Digital Image Computing Techniques and Applications, 1-8 (2012)
- ↑ Point Cloud Library,http://pointclouds.org/